四分位範囲と箱ひげ図。
新しく追加された単元でどんな問題がでるのか気になるところですよね。
この記事では、四分位範囲と箱ひげ図を優しく解説していきます。
＼ 最高級の鉛筆をテストで使おう ／
このページのもくじ
四分位範囲は入試でも出てます
- 令和5年 公立入試 大問1(16)で出題
- 令和6年 公立入試 大問1(16)で出題
四分位数と箱ひげ図が新課程指導要領に追加されてから、埼玉県の公立入試でも連続で出題されています
＼ 最高にかっこいいシャープペンを使おう ／
四分位範囲と箱ひげ図とは
四分位範囲はデータを小さい順に並べて、データの量で4分割しただけだよ！
賢い犬
| 四分位範囲 | 箱ひげ図 |
|---|---|
| たくさんあるデータを ４つに分けた範囲 | ４つに分けたデータを 図にしたもの |
四分位範囲とはたくさんあるデータを４つに分けた範囲のこと。
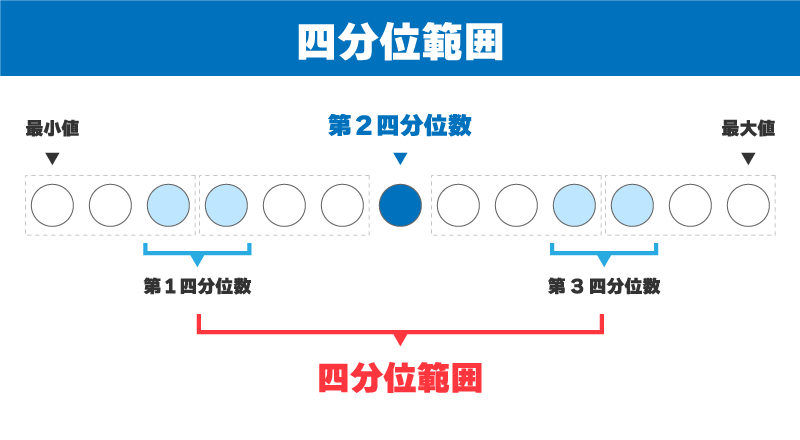
そして、箱ひげ図は４つに分けたデータを図にしたものです。
ここで大切なのが、データの数を基準にしていることです。
コーチ
箱ひげ図でなんとなくデータのばらつきがわかったようなわからないような、、、
たしかにね！箱ひげ図は１つではなく、複数を比較することでばらつき具合がはっきりするんだよ！
賢い犬
数学全体の傾向が知りたい人はこちらもチェック
北辰テストの日程はこちら
四分位範囲と箱ひげ図の特徴
- 簡単にばらつき具合を可視化できる
- 複数を比較できる
- 飛び抜けた1位やビリに影響されにくい
ばらつき具合を可視化
これはわかりやすい特徴ですね。
どの範囲にデータが集中しているのか、どの範囲にデータが少ないのかがひと目見ればわかります。
これはデータの数を基準にして図にしているためですね。
複数を比較
箱ひげ図は複数のグループを比較することで力をさらに発揮します。
例えば、A組、B組、C組、D組のテスト結果を箱ひげ図にすると、点数のばらつき具合がひと目でわかります。
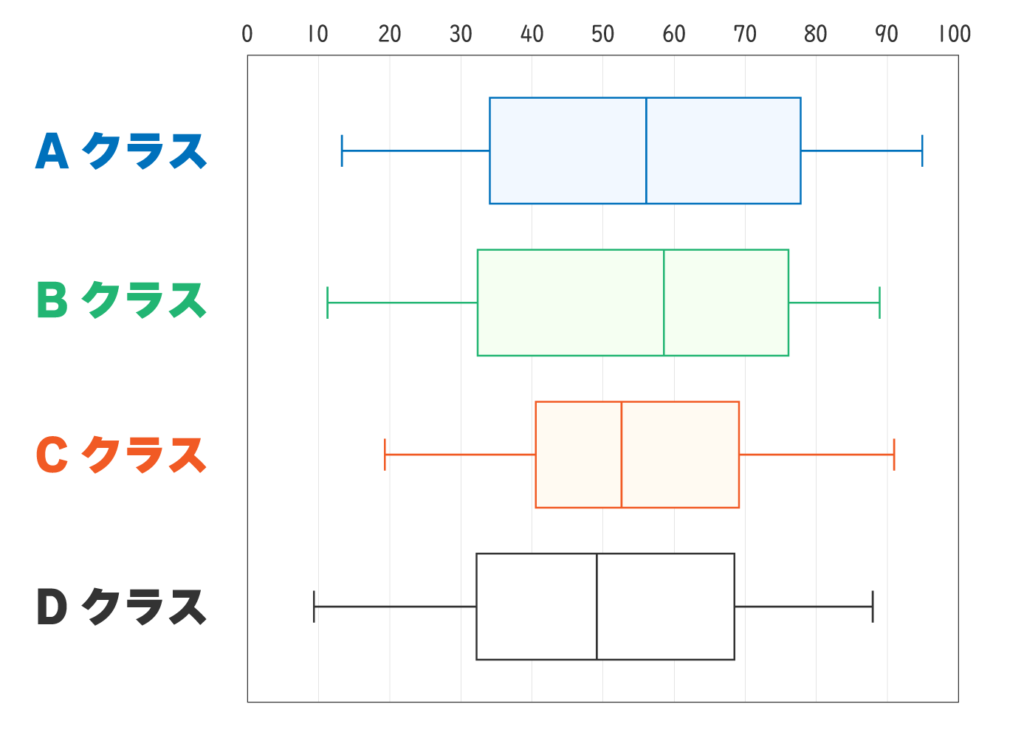
どの点数帯にデータが集中しているのかわかりますね。
点数のばらつきは平均点からはわからないため、箱ひげ図が有効になります。
飛び抜けたデータに影響されない
これはデータの数を基準にしているからですね。
データを比較するときによく使う平均値と比較するとわかりやすいですね。
四分位範囲では平均値は使わずに、中央値（データの真ん中の値）が使われます。
＼ 最高にかっこいいシャープペンを使おう ／
四分位範囲と箱ひげ図の傾向
- 大問1レベル
- 箱ひげ図の性質を聞く問題
- 四分位範囲でわかる値を聞く問題
2022年の出題
| 第1回 | 大問2(3) データから四分位範囲を求める |
| 第2回 | ＜出題無し＞ |
| 第3回 | ＜出題無し＞ |
| 第4回 | 大問1(8) データから四分位数を求める |
| 第5回 | 大問2(3) 箱ひげ図の正誤問題 |
| 第6回 | ＜出題無し＞ |
| 第7回 | 大問1(8) 箱ひげ図からデータの値を求める（選択問題） |
| 第8回 | ＜出題無し＞ |
2023年の出題
| 第1回 | 大問1(10) 箱ひげ図の正誤問題 |
| 第2回 | ＜出題無し＞ |
| 第3回 | ＜出題無し＞ |
| 第4回 | ＜出題無し＞ |
| 第5回 | 大問2(3) 箱ひげ図から数の範囲を求める |
| 第6回 | 大問2(3) 箱ひげ図から平均値を求める |
| 第7回 | ＜出題無し＞ |
| 第8回 | 大問1(10) ヒストグラムからの読み取り |
問題のレベルは難しくない
問題は難しくありません。
教科書に載っている四分位範囲と箱ひげ図の部分をしっかりと読んでおけば大丈夫です。
去年（2021年）から北辰テストの出題範囲となっていますが、初めて出題されたのは2022年4月の北辰テストでした。
そのため、まだ問題数自体が少ないため傾向という傾向はわかりませんが、データの活用の単元は基本問題がほとんどです。
性質を答える
箱ひげ図にはどのような性質があるのか選択する問題が出題されます。
これは2022年2月の公立高校入試でも出題されました。
- データの中に離れた値がある場合、四分位範囲はその影響を受けにくい。
- 四分位範囲は第3四分位数から第1四分位数をひいた値である。
- 箱の中央は必ず平均値を表している→NG中央値を表している。
- 第2四分位数と中央値は必ず等しい。
値を答える
四分位範囲では６つの値を求めることができます。
- 最小値
- 最大値
- 第１四分位数
- 第２四分位数（中央値）
- 第３四分位数
- 四分位範囲（第３ー第１）
それぞれ簡単に求めることができます。
箱ひげ図から説明する
これはまだ北辰テストでは見られませんが、公立入試は令和5、6年と連続で箱ひげ図を使った説明問題を出題しています。
難易度は難しくありませんが、しっかりと四分位数と箱ひげ図の性質を理解しておく必要があります。
四分位範囲と箱ひげ図の解き方
基本的な知識を覚える
北辰テストで出題される四分位範囲と箱ひげ図は基本的な問題が出題される
箱ひげ図からわかる値を覚えましょう。
- 最小値
- 最大値
- 第１四分位数
- 第２四分位数（中央値）
- 第３四分位数
- 四分位範囲（第３ー第１）
最小値と最大値はひげの端になります。
第１四分位数はデータを数でわけた前半の中央値になります。
第２四分位数はデータ全体の中央値です。
第３四分位数はデータを数でわけた後半の中央値になります。
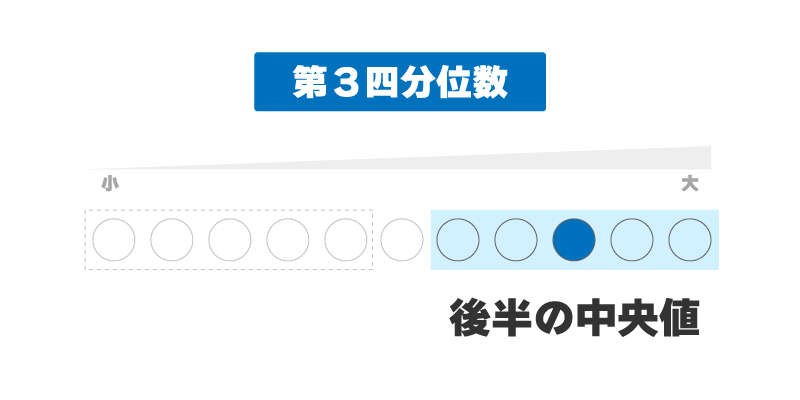
最後に、四分位範囲は
前半の中央値（第１四分位数）から後半の中央値（第３四分位数）になります。
四分位範囲はとにかくデータの数が基準なので「中央値」をよく使います
賢い犬
箱ひげ図の性質を覚える
- データの数を基準にしている
- 離れた値（飛び抜けた1位やドベ）に影響されにくい
- 4つの範囲に分けられている
- 第２四分位範囲と中央値が等しい
- 平均値はわからない
箱ひげ図の性質はとにかく「データの数」を基準にしていることです。
データの数を基準にしているので、データの値には影響を受けにくくなります。
また、４つの範囲に分けるのもデータの数が基準になります。
中央値もデータを小さい順に並べた際に、真ん中にくる値なのでこちらもデータの数が基準になります。
中央値の求め方（基本）
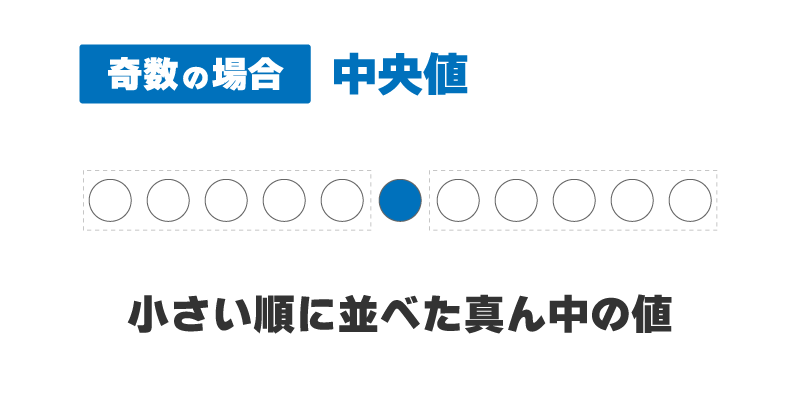
中央値はデータの数が奇数か偶数かで求め方が少し違うので、しっかり頭に入れておきましょう。
四分位範囲では「中央値」の求め方が基本になります！しっかり復習しておきましょう
賢い犬
四分位範囲の求め方（データの数が偶数）
データの数が偶数（たとえば12個）の場合を考えてみましょう。
まずはデータを小さい順に並べます。
並べ替えたデータを4分割します。
分けたあとは、四分位範囲の値を求めます。
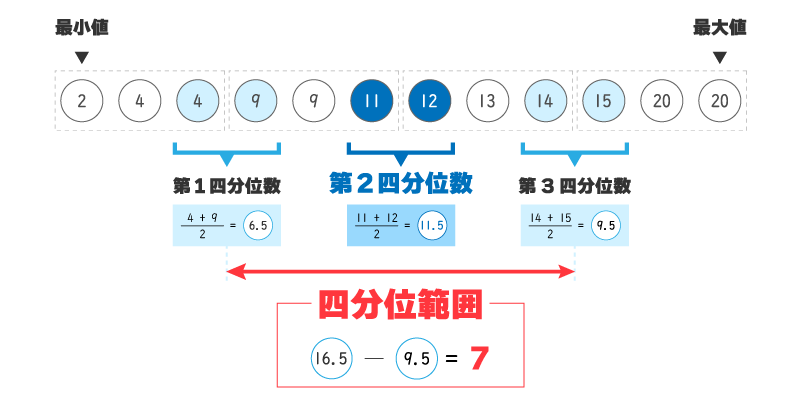
区切りの部分にデータが無いときは、区切りの左右２つの平均が四分位数になるよ！
賢い犬
四分位範囲の求め方（データの数が奇数）
次はデータの数が奇数（データの数11個）の場合を見てみましょう。
同じようにデータを小さい順に並び替えます。
４つに分割します。
このとき、奇数だと１つあまります。
分けたあとは、四分位範囲の値を求めます。
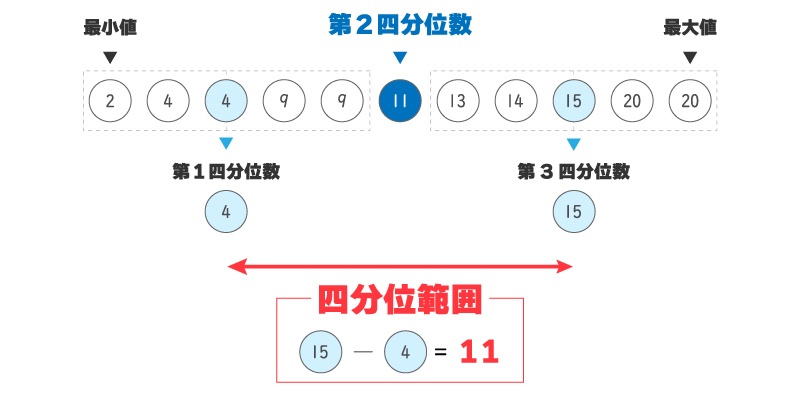
コーチ
奇数の場合は真ん中の第２四分位数（中央値）が簡単にわかりますね
＼ 最高にかっこいいシャープペンを使おう ／
四分位範囲・箱ひげ図まとめ
四分位範囲と箱ひげ図について、解説しました。
北辰テストででる問題が解けるように、基本的なことはしっかり覚えておきましょう。
北辰テストの日程を確認しよう
北辰対策記事
北辰テストの問題解説
