2021年4月25日に北辰テストがはじまりましたね。
今回は1回目なので、試験範囲は狭くなっています。
ただ、北辰テストの数学では幅広い難易度の問題が出題されます。
そこで、今回は難易度が高かった大問4⑶を解説していきます。

コーチ
最後の問題はマジで何をどうしたらいいのかわからなかった、、、
まさにラスボスですね。丁寧に解説をしていくので安心してね

賢い犬
このページのもくじ
大問4はどんな問題?
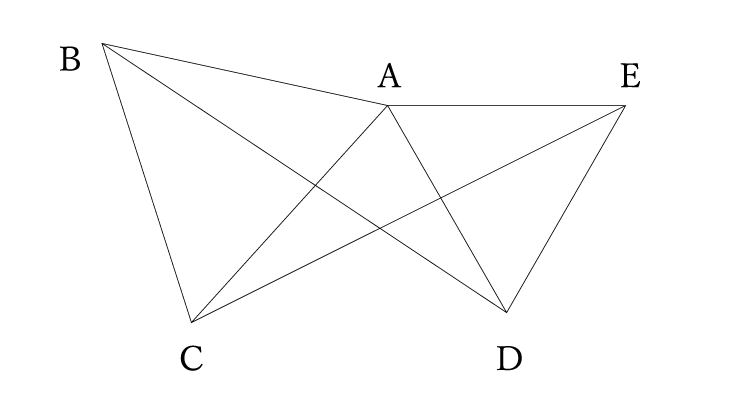
平面図形の問題ですね。この問題でのポイントは正三角形が使われていることです。
⑴では合同。⑵では角度を求める問題。
(1)の証明する部分
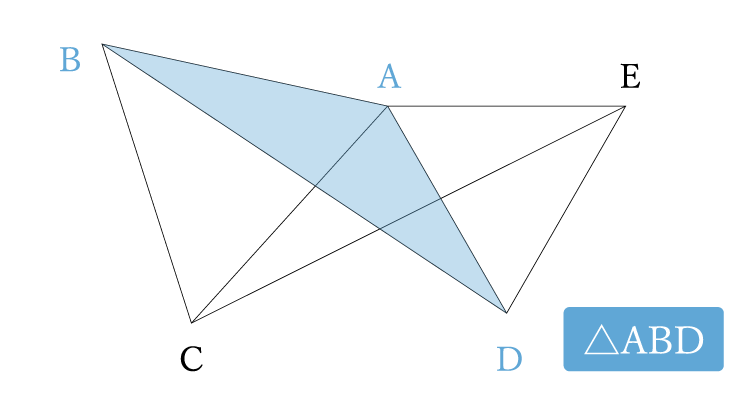
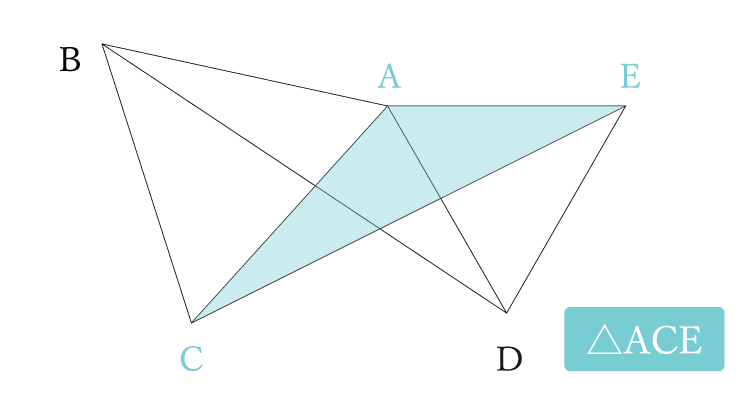
⑴の合同はよくある問題ですね。△ABDと△ACEが合同であることを証明する感じです。正三角形を2つ使った図形では合同になる部分がたくさんでてきます。そのひとつを証明する問題。

コーチ
これは標準的な証明問題だね!
そうだね!同じ長さの辺をしっかり見れば、あとは間の角度を証明して終わりだね!

賢い犬
(2)で求める角度
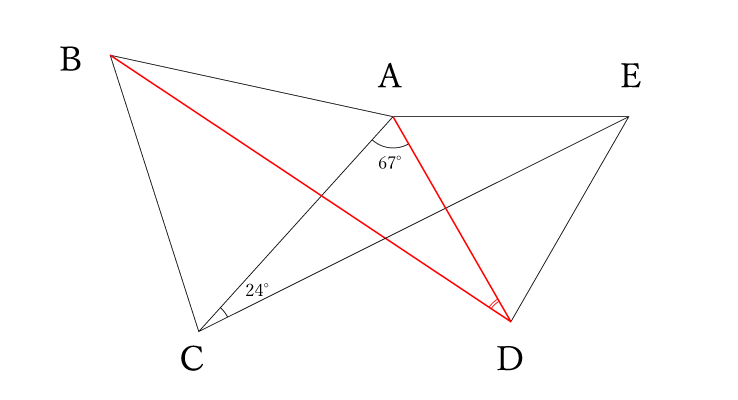
⑵の角度を求める問題は、⑴の合同と正三角形の角度、三角形の内角の和を使って求める標準的な問題でした。
(1)の合同と正三角形の内角はすべて60°を利用すればかんたんに解けますね

賢い犬
(3)で面積比を求める部分
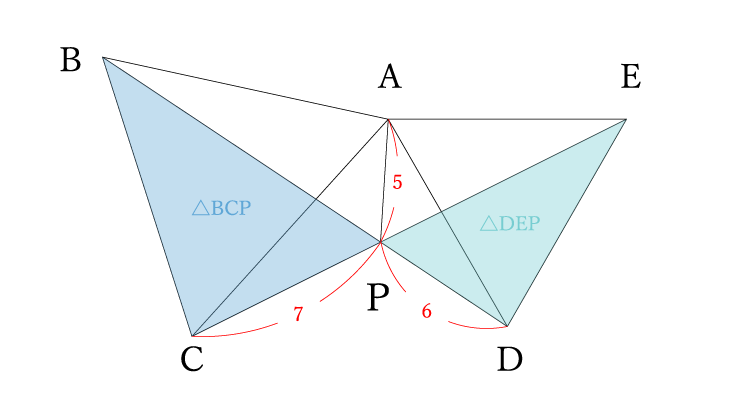
そして、⑶は面積比をもとめる問題。いやぁ〜本当に北辰テストでは面積比を求める問題がよくでますね。
正直、このレベルの問題は求めるのに時間がかかるので、捨て問にしてもいいと思いますが、解けると気持ちがいいので挑戦していきましょう。
ただ、今回は解答に説明文が必要ないので、ひらめいてざっと計算してしまえば10分かからないかもですね!

賢い犬
大問4⑶の解説をしていくよ

まずは、答えまでの道筋の確認、そしてポイントをみてみましょう。
- 補助線を引くこと
- ⑴の合同を使うこと
- 他の合同な図形を見つけること
- 高さが共通の三角形の比は面積比に比例すること
- 二等辺三角形の底角は等しいこと
笑っちゃうくらいポイントがありますね。
どれも1つ1つみたらわかりそうですが、複合的に組み合わさっているのでわかりにくくなってますね。
次は答えまでの道筋ですね
- STEP
わかる角度を書いていく
まずはわかるところを記入していくことで解法のヒントを探していきます。
- STEP
補助線を引いて分かっている長さを使う
与えられた条件を有効的に使えるように補助線を引きます。今回は正三角形になる補助線です。
- STEP
合同な図形を見つけて分かっている長さを使う
補助線でできた正三角形から他の部分にも合同な図形ができたことに気付けるかどうか。
- STEP
補助線を引いて三角形の面積比を出す
長さがわかった部分を使って面積比を求めるために、さらに補助線を引きます。
- STEP
共通の面積から問題の面積比を求める
一筋縄ではいかない面積比は共通部分をうまく使って面積比を出していきます。
いやぁ〜道筋までも長いですね。
基本的な知識でわかるところをとにかく書いていき、分かっている長さを有効活用していきます。
面積比とくれば高さが共通の底辺の比を使うので、そこまでどうやって持っていくかがカギになります。
問題を解くためのポイントと道筋をしっかり確認しておきましょうね

賢い犬
ステップ⓪ 分かっている条件を書き出してみる
問題文からわかること
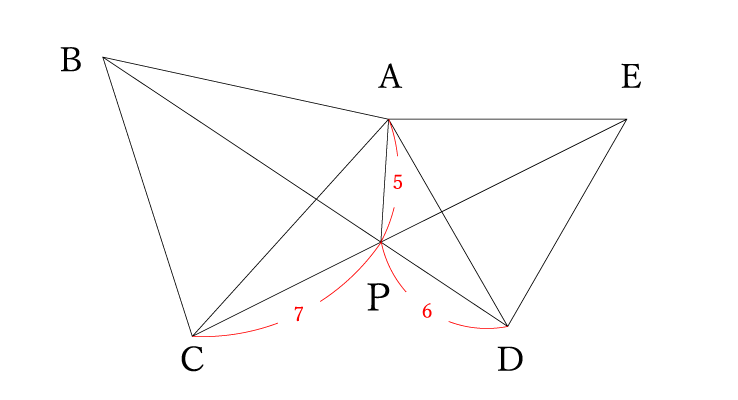
- AP=5cm
- CP=7cm
- DP=6cm
正三角形の条件からわかること
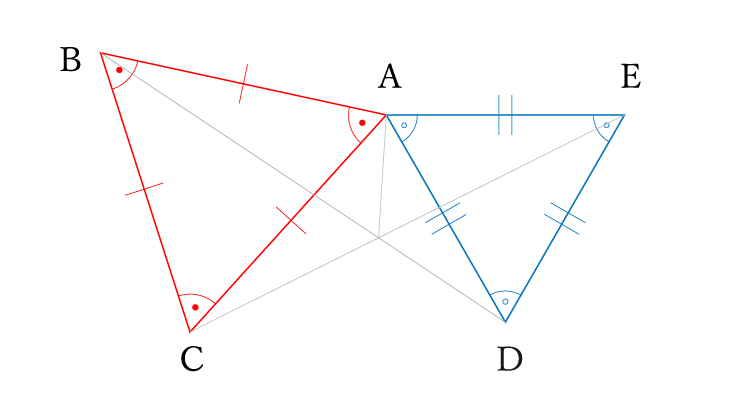
- AB=BC=CA
- AD=DE=EA
⑴からわかること
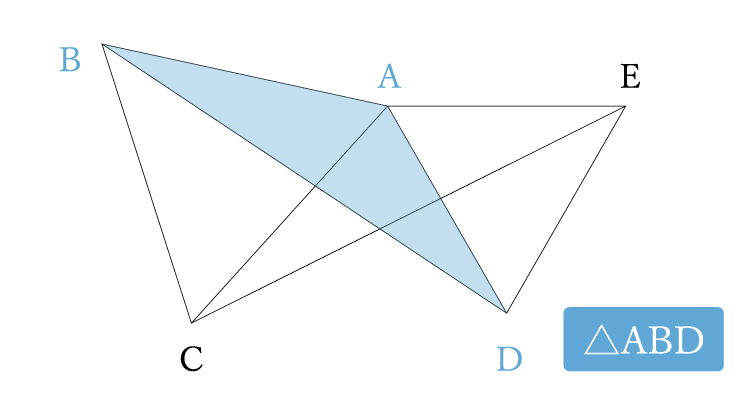
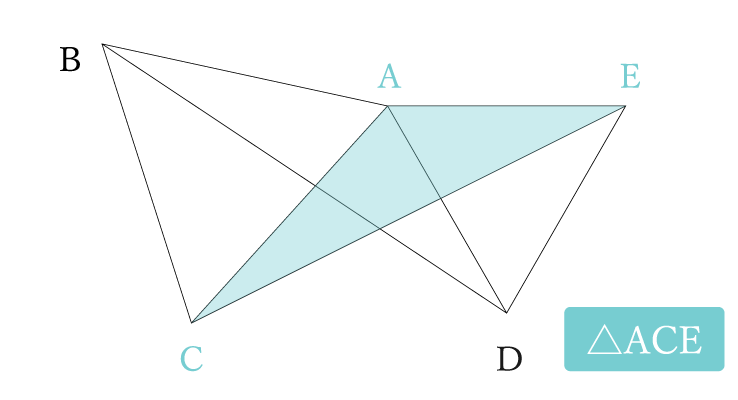
- △ABD≡△ACE
求めるのは
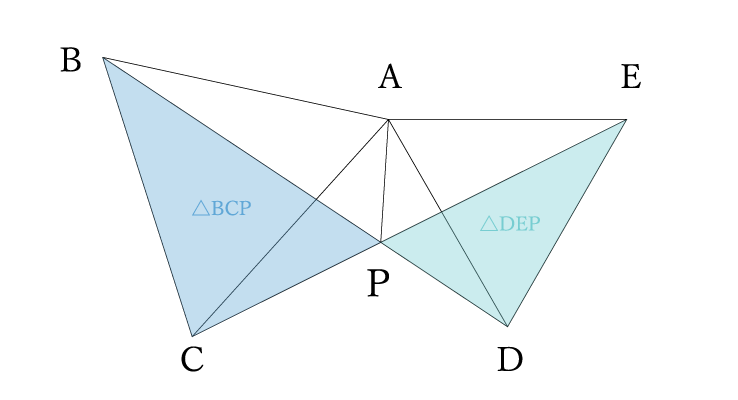

コーチ
よっしゃ!難問もこのステップなら解けるんだね!
長えから覚悟しろよ

賢い犬

コーチ
急に口わるいなぁ
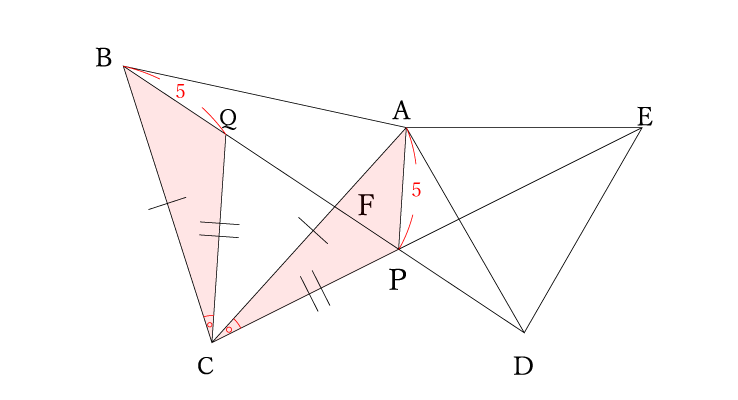
ステップ① わかる角度を書いていく
まずは2つの正三角形の角度がわかりますね。それぞれ60°です。
そして⑴の合同から△ABD≡△ACEなので、それぞれの角が等しいことがわかりますので、書き込んでいきます。
ここで、交点となっている部分に記号をつけましょう。線分ACと線分BDの交点をとりあえず点Fとします。
点Fにおいて対頂角は等しいので、それも書き込んでいきます。
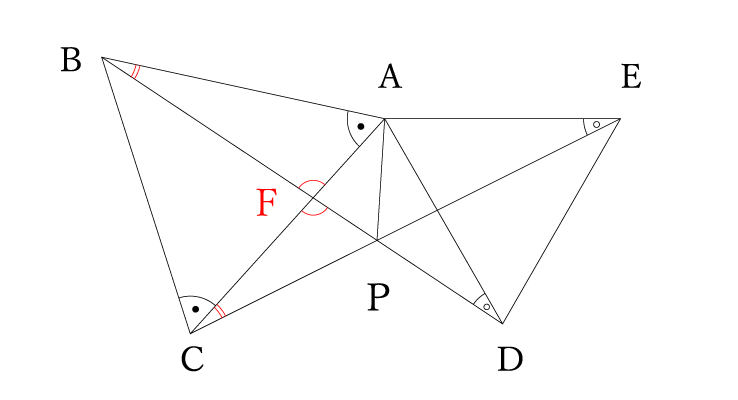
すると△FBAと△FCPの2つの角度が等しいことがわかり、残りの角度も等しいことがわかります。
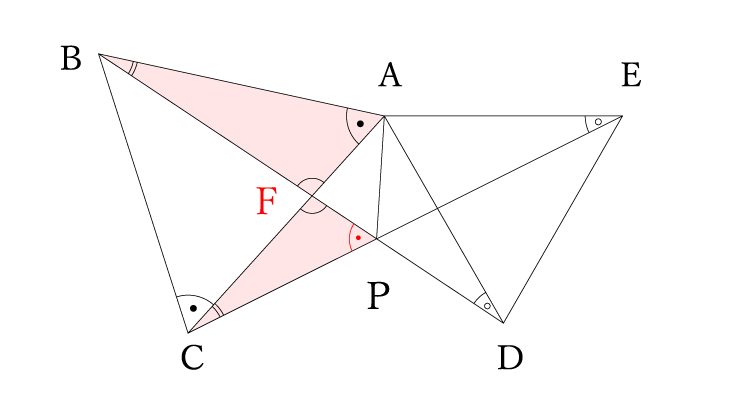
正三角形より∠BAC=60°よって∠BPC=60°となります。
こんなところも60°だったんですね。

コーチ
そこが60°とわかってどうなるの?
慌てない慌てない。正解を導くための大切なステップだよ

賢い犬
ステップ② 補助線を引いて正三角形を作る
CP=7cmという条件が分かっているので、これを有効的に使える補助線を引く。
点Cから線分BP上に線分CPと同じ長さになるように補助線を引きます。
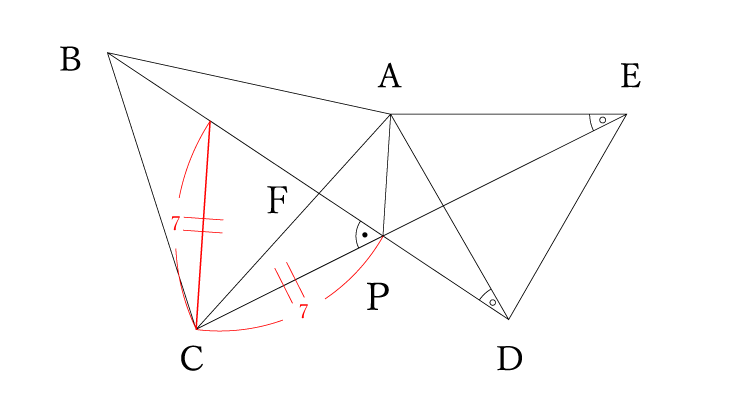
もう本当にこれは問題をどれだけこなしたかで閃くかどうかですね。天翔る龍の閃きレベル。
この補助線と線分BPの交点をとりあえず点Qとすると
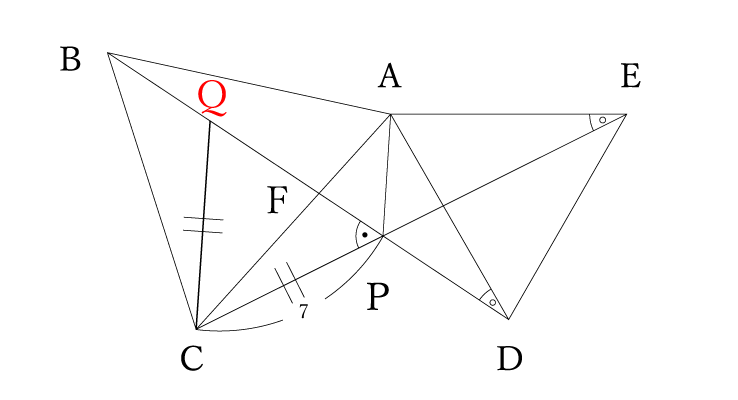
CP=CQ
となりますね。そしてこの補助線でできる△CPQに注目していきましょう。
CP=CQなので、△CPQは二等辺三角形。二等辺三角形の性質より、底角は等しくなるので
∠QPC=∠PQC=60°
となります。
そして△CPQの内角の和より
∠PCQ=180°+(∠QPC+∠PQC)=60°
よって、△CPQはすべての角が60°で等しいので、正三角形になります。
つまり
CP=CQ=QP=7cm
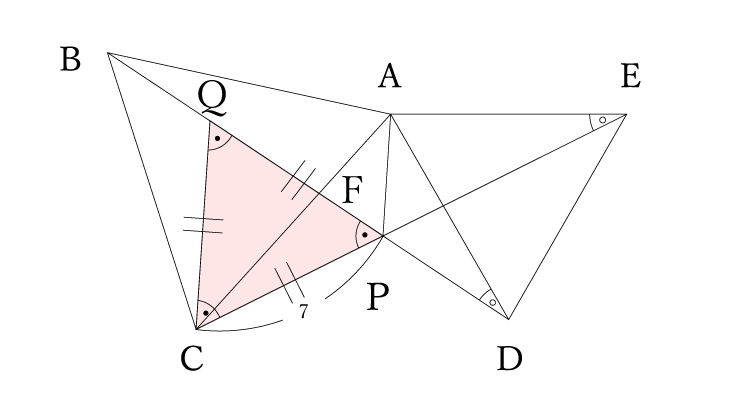
何やってんのこれ?って思うかもしれませんが、これをしないと次に進めません。
一本、補助線を引くだけで正三角形をつくる!これがヒラメクかどうかだよ!

賢い犬
ステップ③ 合同な図形を見つける
線分BDの長さがわかると面積比がふわっと分かってきそうですね。
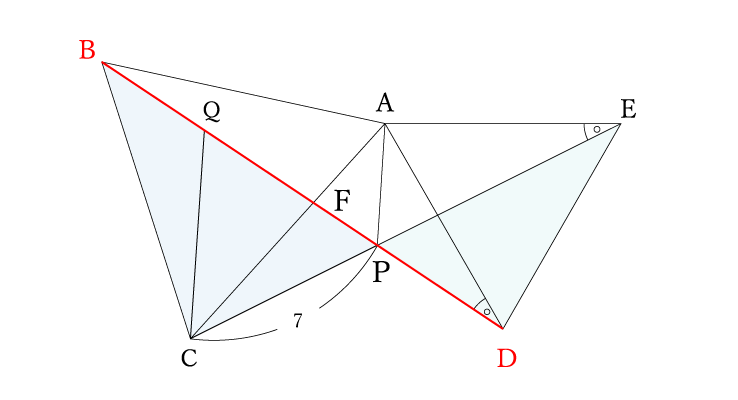
「線分BDがわかると面積比を求めることができそうだな」と想像できることが大切です

賢い犬
そこで、線分BDの残りで分かっていない線分QBを求めていきます。
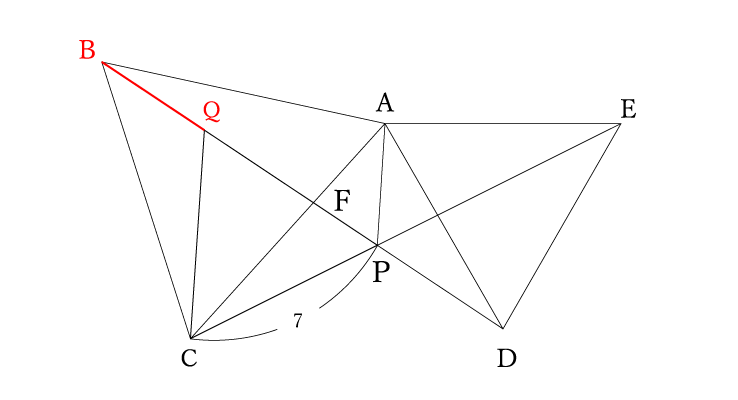
線分QBを含む△CQBに注目します。
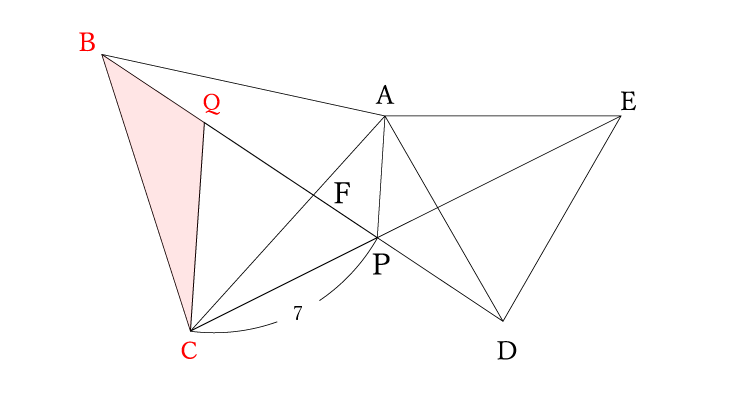
△CQBの2辺は2つの正三角形(△ABCと△CPQ)の辺というのがわかります。
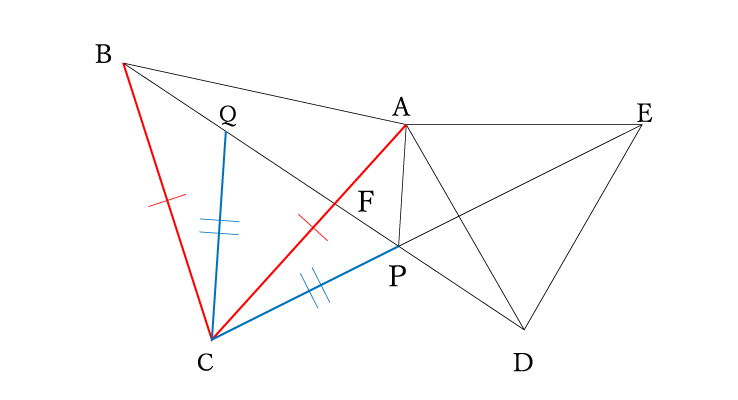
これと共通している三角形を探すと、、、△CPA!こいつが合同っぽいですね。
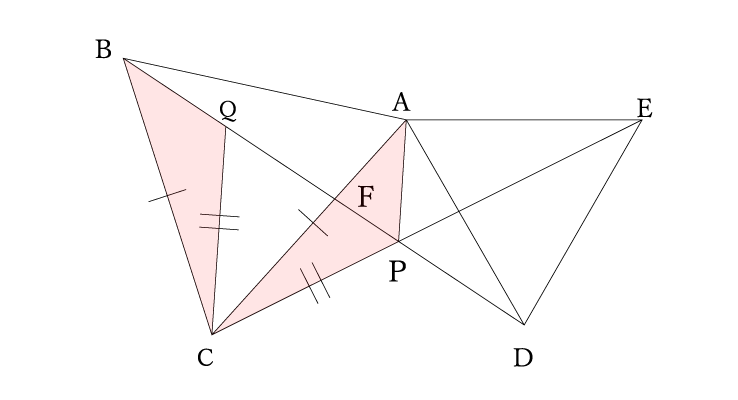
あとは三角形の合同条件である「二組の辺とその間の角がそれぞれ等しい」を使えれば合同を証明できますね。
しかも△CPAは線分PA=5cmとわかっているので、合同の証明さえできれば残りの線分QBの長さがわかりますね。
正三角形より
∠BCA=∠PCQ=60°
∠BCQ=60°-∠QCF
∠ACP=60°-∠QCF
すなわち∠BCQ=∠ACPよって△CQB≡△CPAとなります。
これより
QB=PA=5cm

コーチ
おぉ~気持ちいいくらいに線分BDの長さがすべてわかったね!
ステップ④ 補助線を引いて面積比を出す
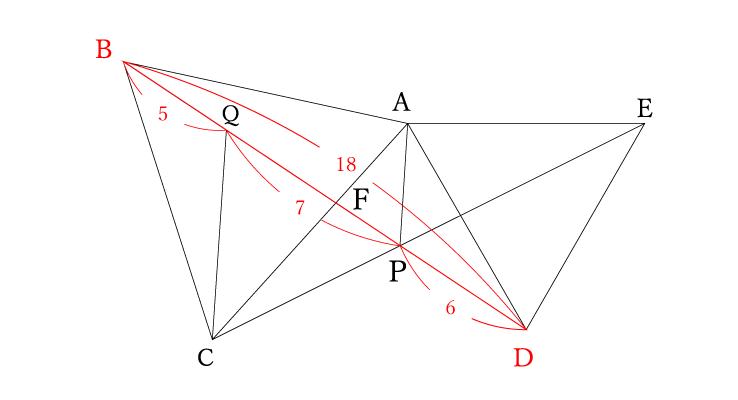
今までのステップ①〜③で線分BPの長さがわかりました。条件から線分PDもわかっているので、この長さを使って△BCPの面積を表現していきましょう。
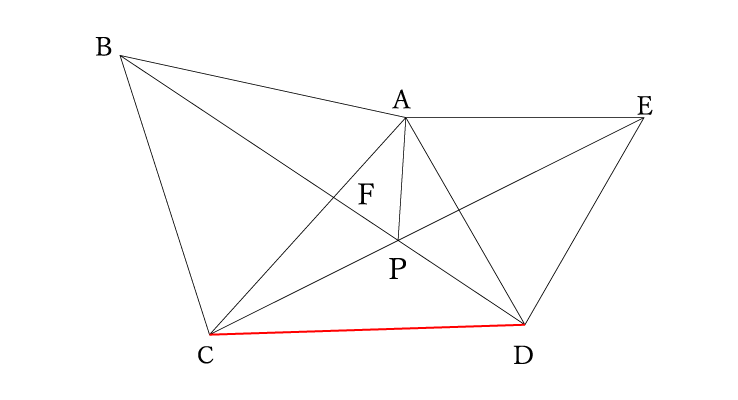
補助線は点Cから点Dに引きます。
その前に説明しやすいよくするために△BCPの面積をS1、△DEPの面積をS2、△CPDの面積をS3と置いておきます。
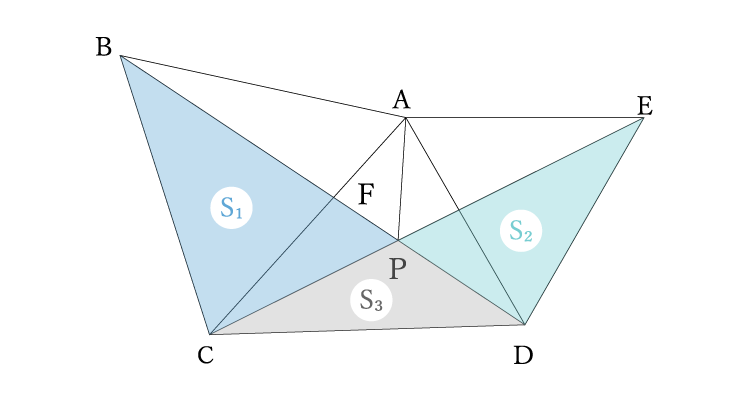

コーチ
BDの長さがわかったからあとは面積比を求めるだけだね♪
線分CDを引くことでS3をはさんでS1とS2の比を求めるよ

賢い犬
△CDBに注目
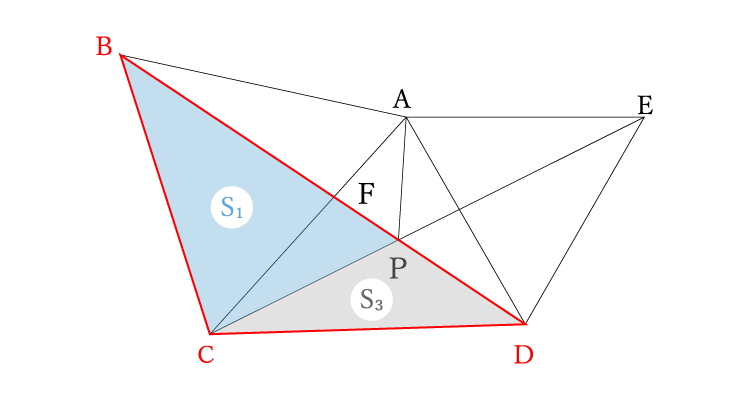
△CDB=△BCP+△CPD=S1+S3
ここで高さが等しい三角形の面積比は底辺の比に比例することから、線分BPと線分PDの比が面積S1と面積S3の比に等しいので
BP=BQ+QP=5+7=12cm
PD=6cm
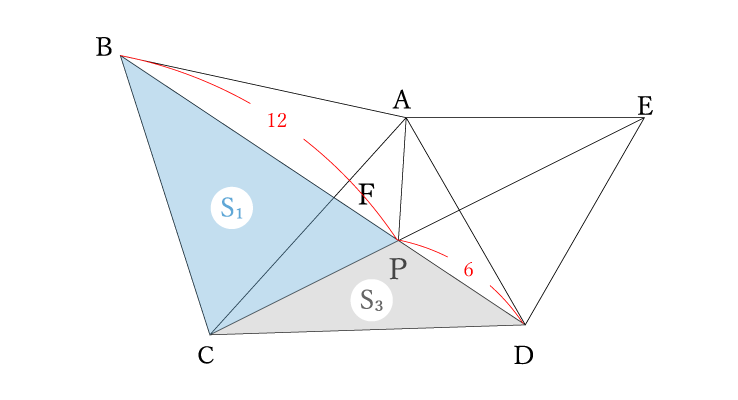
よって
BP:PD=S1:S3=12:6=2:1
整理すると
S1:S3=2:1
△DCEに注目
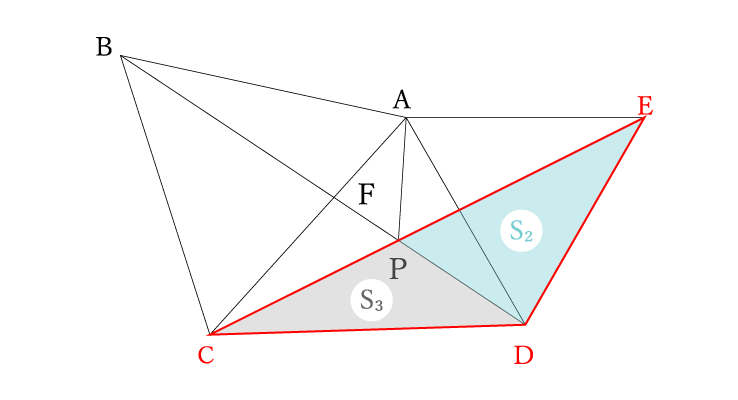
△DCE=△DEP+△DCP=S2+S3
⑴の合同よりBD=CE=BP+PD=12+6=18
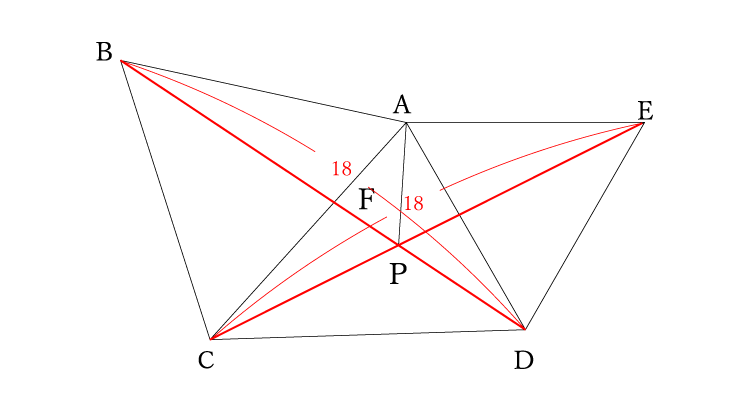
ここで(1)の合同が生きてくるのは素晴らしいですね!

賢い犬
CE=18cm、CP=7cmより
PE=CE-CP=18-7=11cm
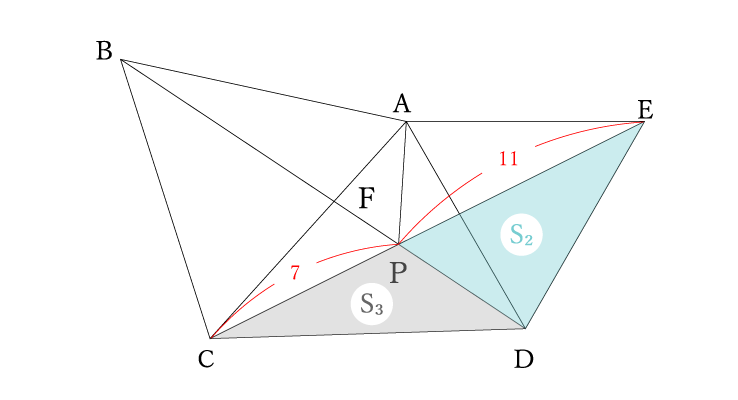
ここで高さが等しい三角形の面積比は底辺の比に比例することから、線分CPと線分PEの比が面積S3と面積S2の比に等しいので
CP:PE=S3:S2=7:11
整理すると
S3:S2=7:11
ステップ⑤ 共通の面積から比を求める
共通の面積は△CPD。つまりS3です。
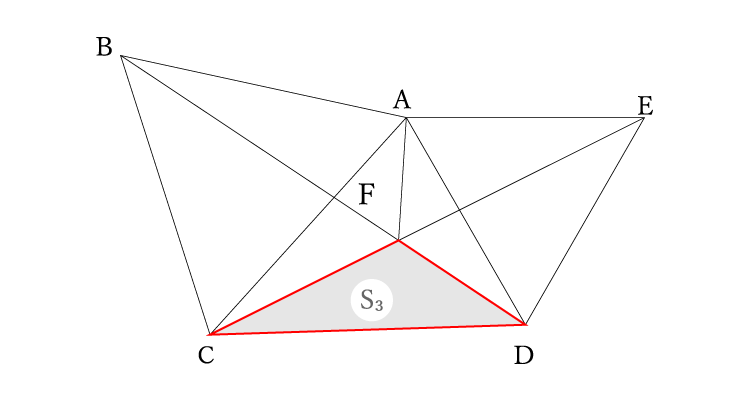
S1とS2をS3を使って表現していき、比を求めます。比で表現すればS3は最終的に消えます。
S1:S3=2:1より
S1=2S3
S3:S2=7:11より
S2=(11/7)S3
求めるのはS1:S2なので
と面積の比を求めることができました。

コーチ
できたできた~!
すごく長い解説を最後までよくついてこれましたね。面積比の問題のの中でも難しいので良い力試しになりますね

賢い犬
この問題をもう少し考えてみる
この問題では、正三角形が主役ですね。
これは中学二年生の図形の分野で習った正三角形の性質をちゃんと理解していないと解けません。
そして、補助線。これは数学にハマりはじめないと見えてこないテクニック。
今回は特に二等辺三角形(最終的には正三角形)を作るように補助線を引くので、問題を作った人からの「正三角形をうまく使ってね〜」という声を聞き取ることができるかどうかですね。
図形の中でも面積比の問題は難易度がグッとあがります。
問題を作った人は単純な公式だけではなく、平面図形の性質自体を理解しているのか問いかけるのに最適な問題となっています。
北辰の過去問にも似たような問題がたくさんあるから、受験生は必ず購入して慣れておきましょう

賢い犬