「作図」これを攻略しないことには偏差値60超えはなかなか見えてきません
しかし
作図を得意と考えてる人はとても少ない、、、
わたしが教えている生徒もほとんどの子が「作図か~」と頭を悩ませていることが多いです
多くの中学生が苦い意識をもっている作図
逆にこれはみんなと差をつけるチャンスです!!
そこでこの記事では作図を解くためにいちばん重要な基本テクニックを4つ紹介したいと思います
このページのもくじ
北辰テストの作図問題とは
- コンパスを使った問題
- 大問2の(1)で出題
- 配点は5点
- 部分点あり
- 難しい問題は年に1,2回
コンパスを使って問題を解くのが作図問題です
この作図問題は大問2の一番最初に出題され、配点は5点
部分点もあります
難易度は簡単なものが80%くらいで難しいものが20%くらいの割合で出題されます
偏差値55くらいを目指す人は部分点は確実に取るようにしましょう!
偏差値60以上を目指す人にとって作図問題は必答です
出題形式
- 文章で説明されたものを作図する
- 2本以上の線を引く
学校のテストで出題される作図問題よりも長い文章で問題が出されます
作図が苦手な人は問題の文章量を見ただけで「オエ」っとしちゃうかもしれません
ただ、問題の意味がわかればめちゃくちゃ簡単なときも多いので問題文の読み方もしっかり確認しておきましょう
また、北辰テストでは簡単な線を一本引けばおしまいの問題はあまりでません
ほとんどの場合は2本以上の線を引いて答えを出す必要があります
特に4回目以降の北辰テストでは作図が難化する印象です
まずは基本テクニック、そして出題パターンを練習していくことが作図の攻略方法になります
作図の基本テクニック4つ
作図をするときに使う基本中の基本のテクニックを4つ紹介します
- 線の二等分線
- 角の二等分線
- 垂線
- 等しい距離
どれも基本的なものですが、北辰テストでの出題のされ方をしっかりと確認しておきましょう

賢い犬
線の二等分線(中点)
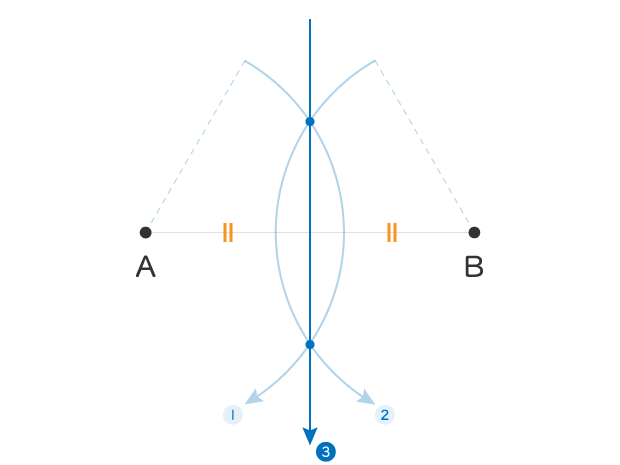
線分ABを真っ二つに分断する線が「線の二等分線」です
ただしくは線分の二等分線ですが、覚えやすく線の二等分線と覚えておきましょう
点と点を結んだものを線分といいますね!

賢い犬
線の二等分線の特徴
- 中点がわかる
- 線の二等分線は常に2点A,Bから等しい距離にある
- 円の中心を知ることができる
- 回転の中心を知ることができる
一番基本的なところは
線の二等分線を引けば中点がわかります
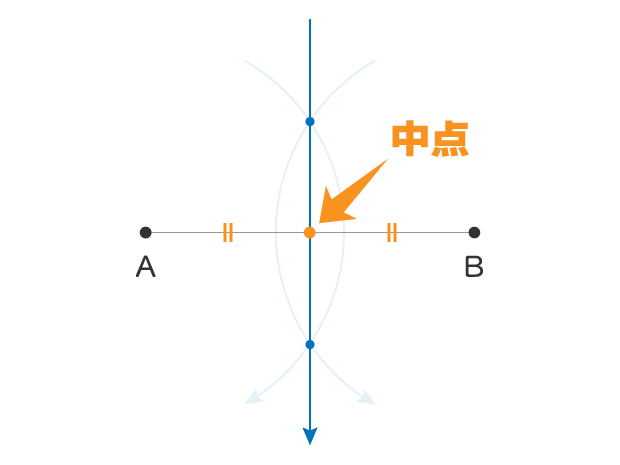
点Aからも点Bからも等しい距離にある中点を見つけることができます
そして線分ABと線の二等分線は垂直に交わっています
これは基本的なことですがとても大切
問題文では
という様に書いてあるので、そのときは線の二等分線を引きましょう
さらに、これは線分ではなく2点A,Bであるときにもあてはまります
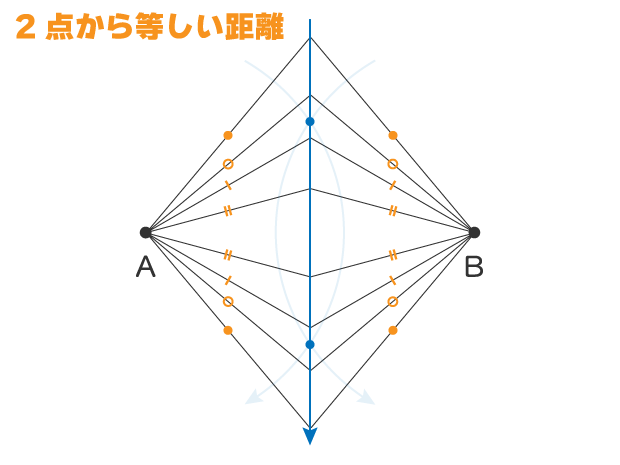
このように2点A,Bに線の二等分線を引くと
どこでも常に点A、点Bから等しい距離になります
そう、線の二等分線とは2点から等しい距離にある点が集まった線なんです
はい、自分で言っていてややこしくなってきましたw
とりあえず問題文に
があれば線の二等分線を引きましょう
線の二等分線を使えば円の中心を求めることもできます

適当に3つの点があります
この3つの点でそれぞれ線の二等分線を引くと
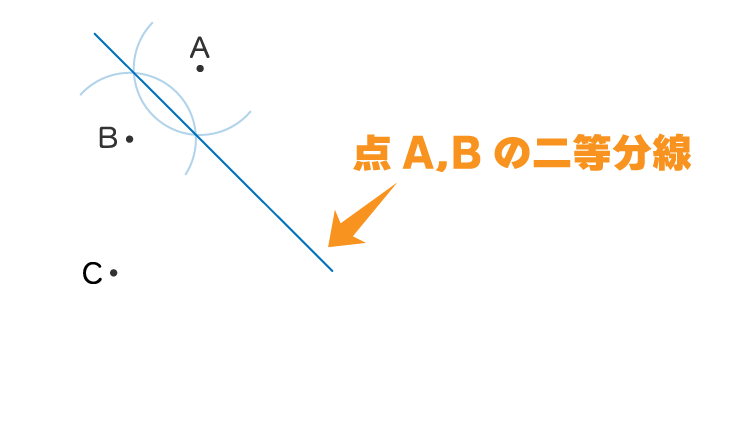
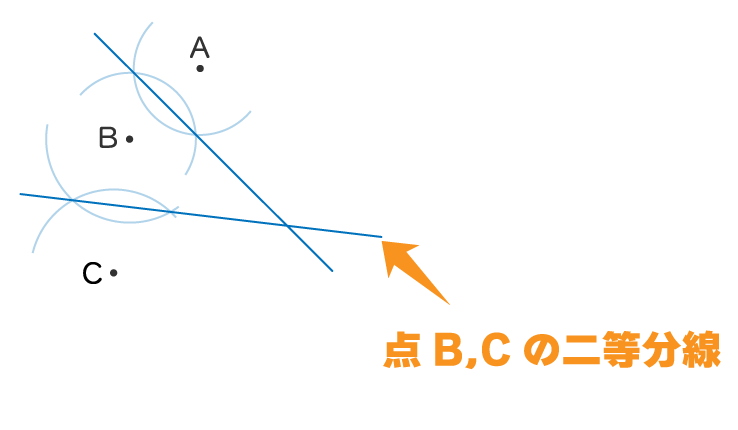
このように一点で交わります
そこが3点を含む円の中心になります
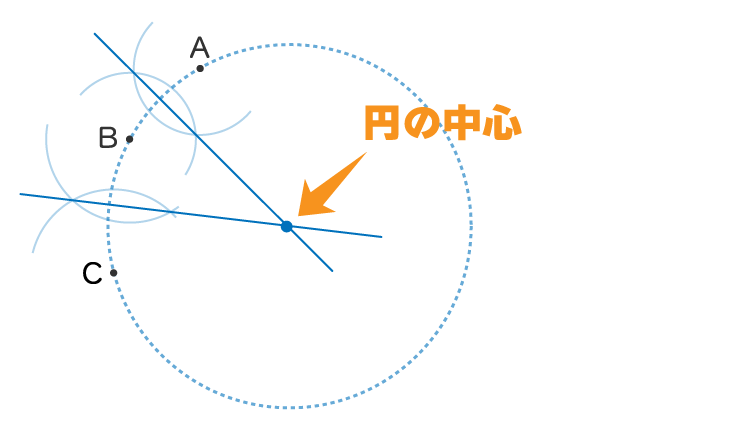
これは円の半径が常に等しいことを利用して作図していますね
点A,Bの二等分線は常に2点から等しい
点B,Cの二等分線は常に2点から等しい
つまりこの2つの二等分線が交わった一点は3点A,B,Cから距離が等しいですよね
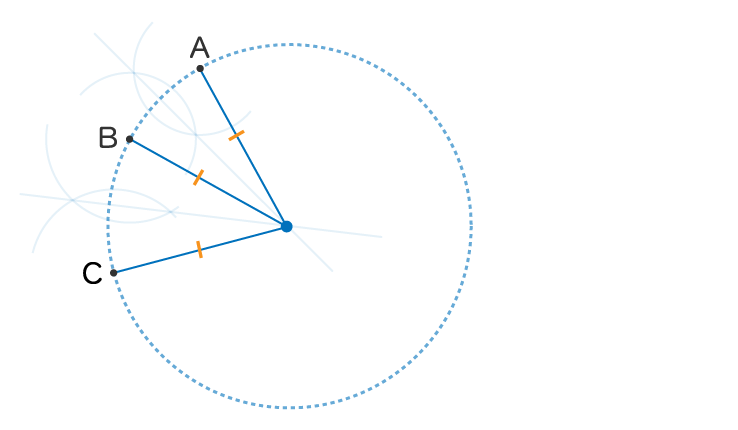
よって2つの線の二等分線が交わった点が円の中心になります
問題文では
ときたら線の二等分線を2つ引いて交点を見つけましょう
円の中心と似ているもので
回転の中心というものがあります
線の二等分線ではこの回転の中心も求めることができます
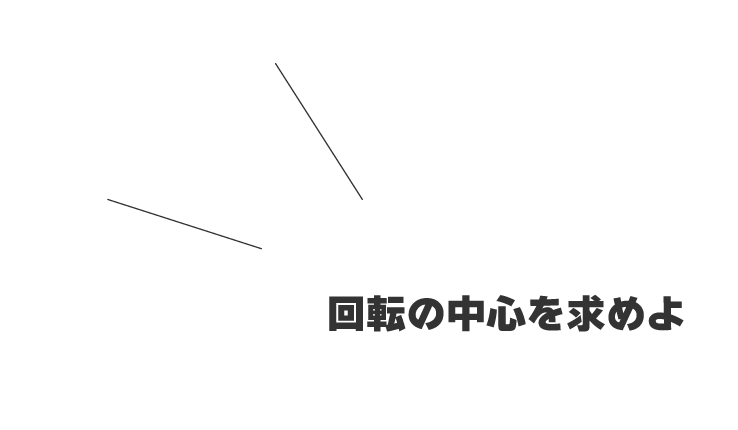
例えばこんな感じに線分が回転したときの回転の中心をもとめる問題は
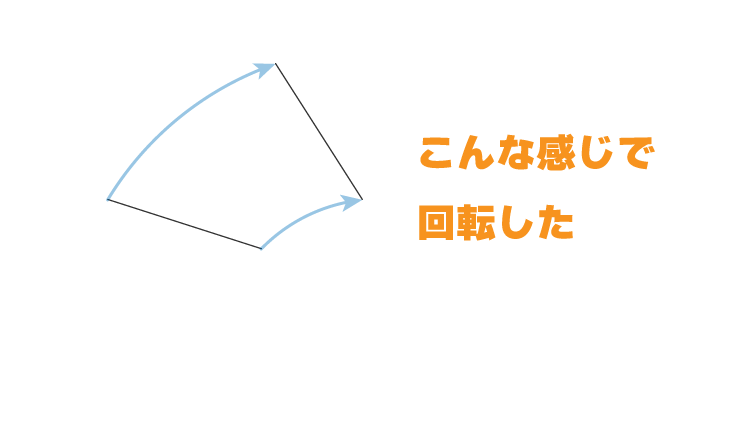
手前の端と奥の端の二等分線を引けば回転の中心を求めることができます
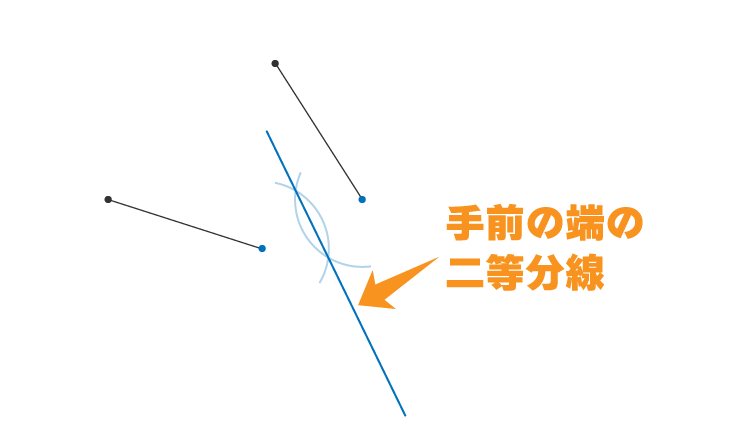
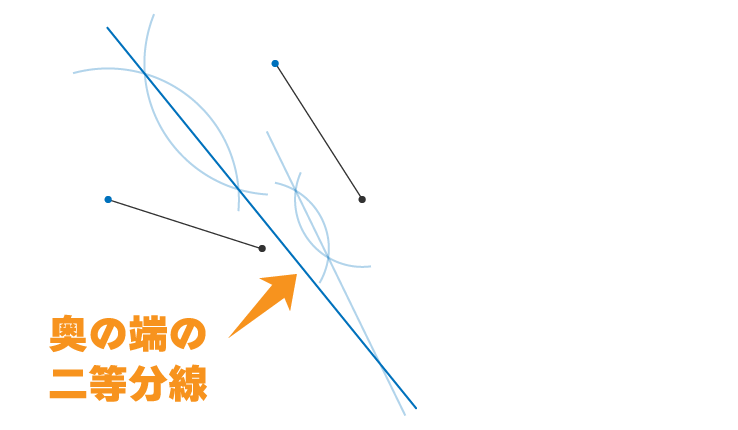
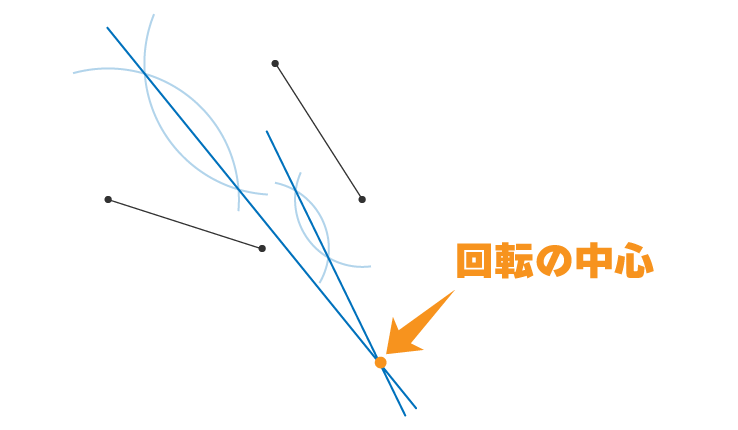
よって2つの二等分線の交点が回転の中心となります
問題文では
と問われます
他にも線の二等分線を使う場面は
- 「点Aを点Cに折り曲げたときの折り目の線分を~」
- 「面積が等しくなるように~」
- 「ひし形を作図しなさい~」
などいくつかあります
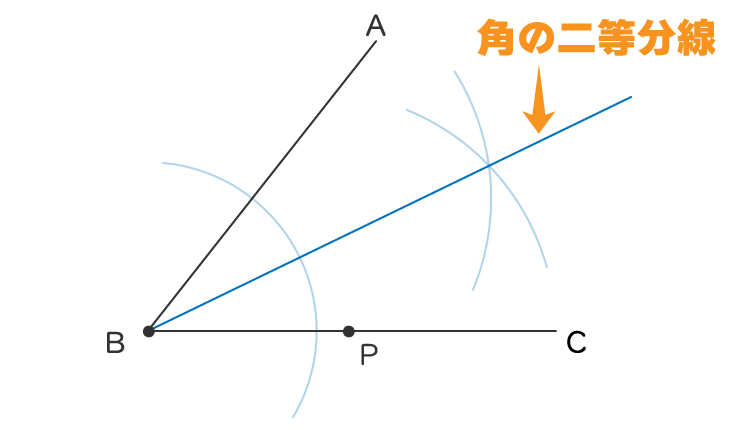
角の二等分線
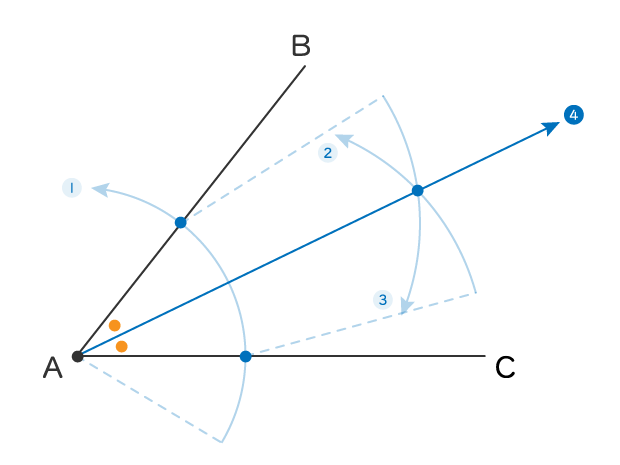
∠BACを真っ二つに分断する線が「角の二等分線」です
角の二等分線の特徴
- 2辺から常に等しい距離
- 接線の円の中心
角度を2等分したときの特徴で一番良く出るのは
角を作っている2つの辺から常に距離が等しくなることです
こんな感じで角の二等分線は辺ABと辺BCからの距離が等しくなります
そして北辰テストの問題文では
「∠ABCを2等分する線を引きなさい」みたいなストレートな言い方をするのはレアケースです
よく出る言い方は
これです

コーチ
2辺~距離等しい、ときたら「角の二等分線」ですからね!
角の二等分線は線と円が接するときの作図でも使います
例えばこのような問題
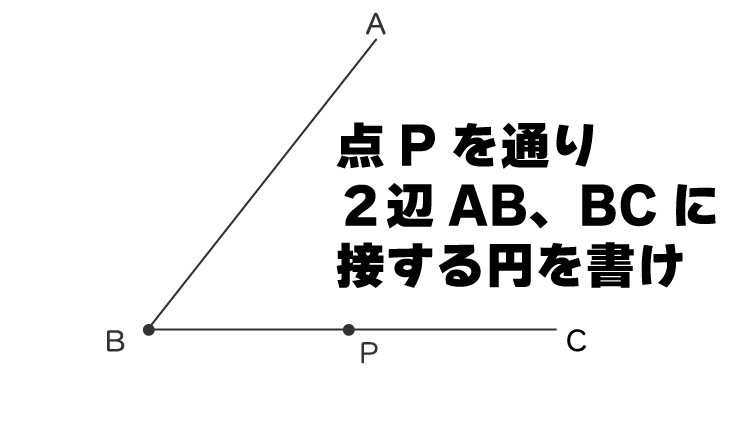
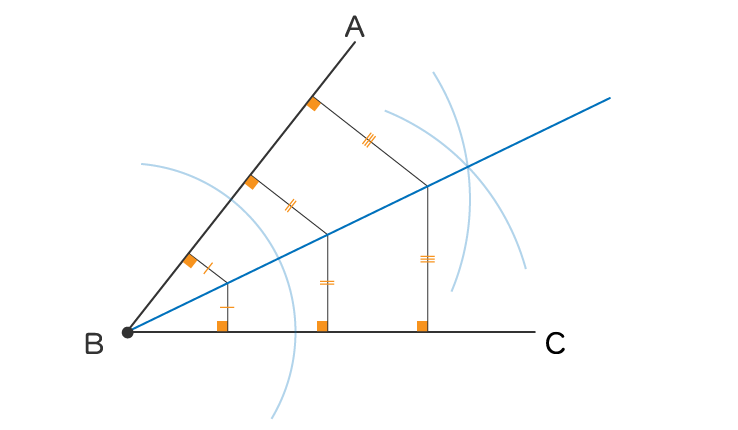
2つの辺に接する円を書くときです
まずは角の二等分線を引きます
角の二等分線は常に2つの辺から距離が等しいです
ここで、円の半径は中心からいつも等しいことを考えると
2つの辺に接する円の中心はこの角の二等分線上にあることがわかります
そしてもう一つの条件となる点Pを通るので
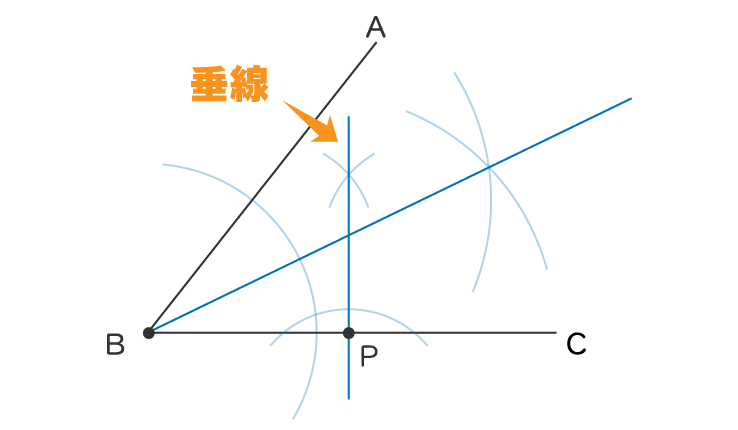
このように垂線(あとで説明)を引くと
この交点が円の中心となります
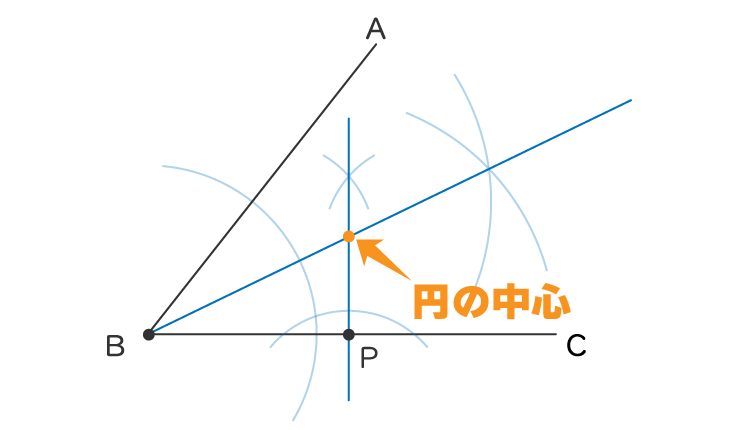
円の中心から接点に線を引くと
接線と垂直に交わるため、接点からの垂線上に円の中心があります
よって、交点が円の中心と確定したので
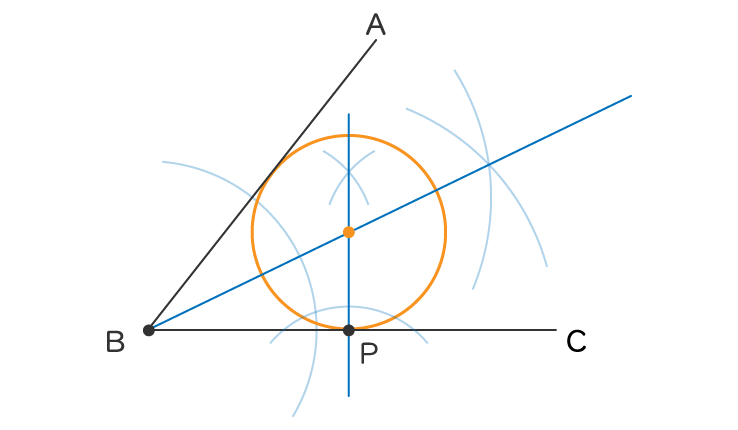
点Pを通り、2つの辺に接する円が完成します
いや~円が関わってくると少し複雑になりますね
問題文の出し方は
みたいな形で出題されます
垂線
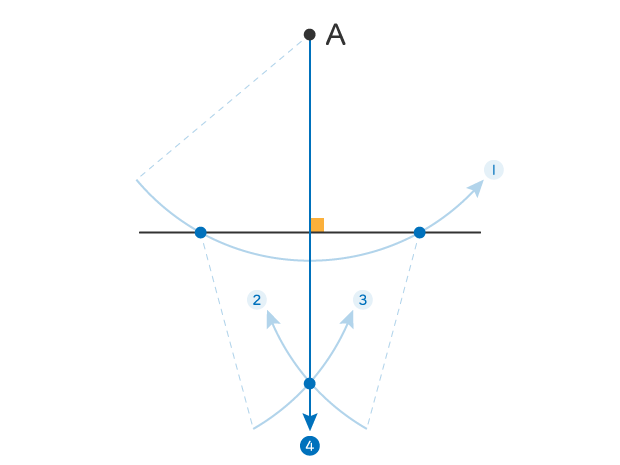
点と線だけで無から90度をつくりだすこれが垂線です
垂線にはポイントが2つあります
表向きは「90度」というわかりやすい特徴
そして裏に隠れた「最短」という特徴もあります
最短の問題はたま~に出るからね

賢い犬
垂線の特徴
- 90度をつくる
- 最短
- 接線
まずは垂線といえばの90度ですね
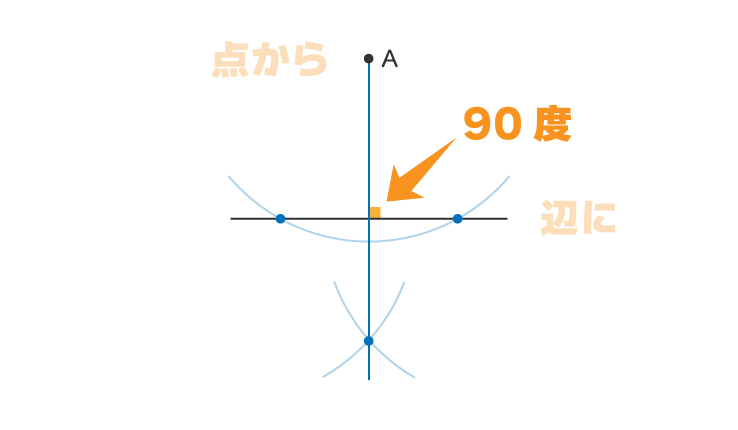
点から辺に垂線を引くことで90度をつくりだします
問題文では
と少し言い換えた問題の出し方になります
次は最短です
最短にはざっくり2つのパターンがあるのでそれぞれ見ていきましょう
- 点→線への最短
- 点→線→点への最短
点から線への最短
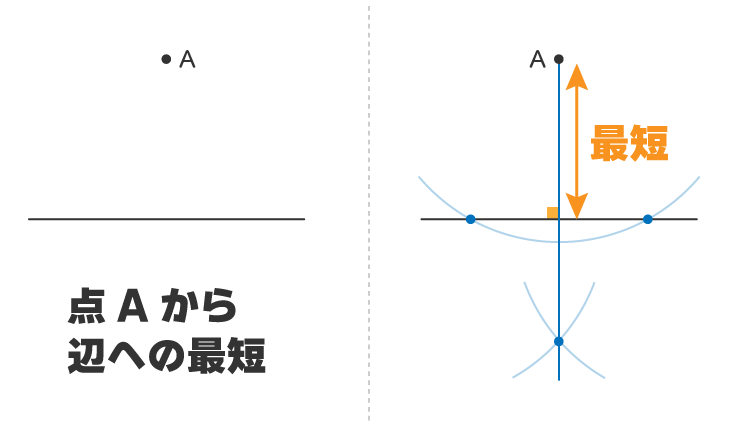
これはシンプルに垂線を引くだけの問題ですね
点から線、線から点への最短
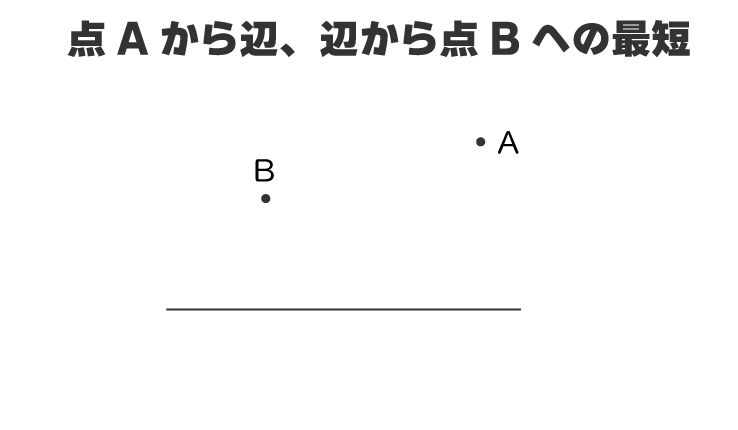
こういった問題です
まずは点Bから辺に対して垂線を引きます
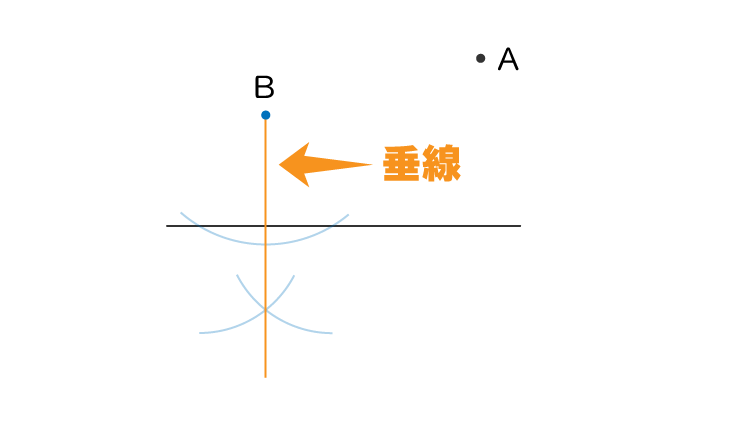
次に辺対象となる点B’を作図します
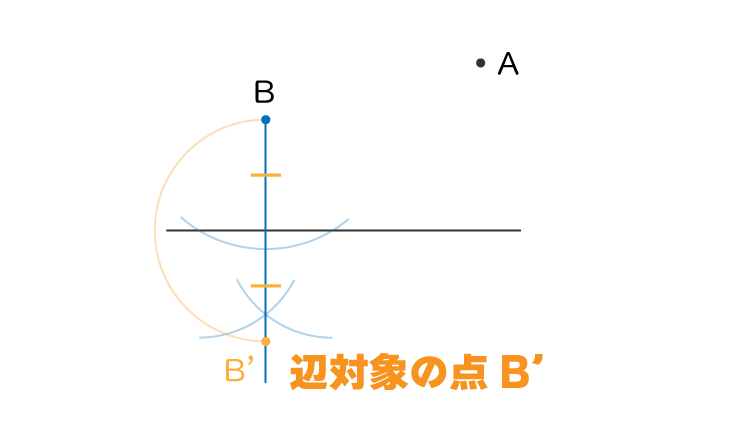
点Aから点B’に線を引きます
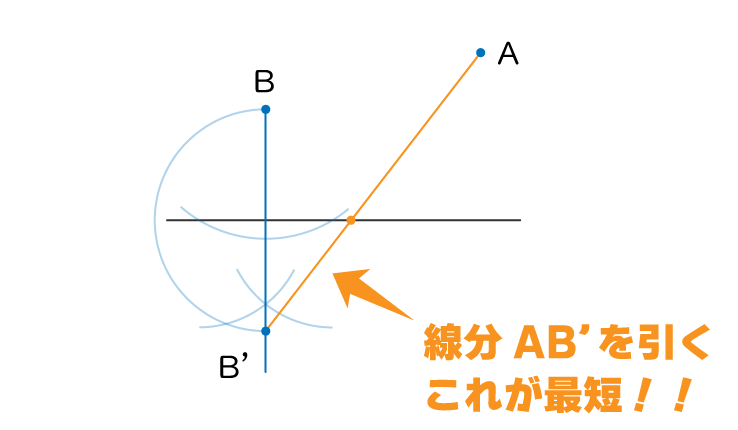
点Aから点B’までの最短距離は直線で結んだときですよね
ここで
点A→辺→点Bの最短距離と点A→辺→点B’の最短距離は等しくなります
線分AB’と辺との交点Cから点Bに線を引くと
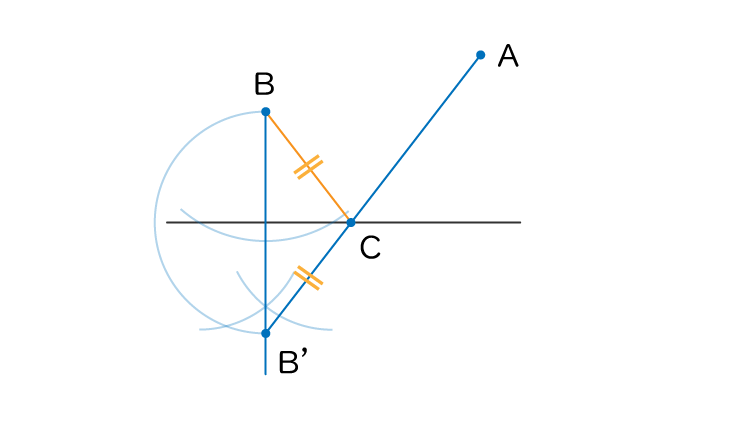
BC=B’Cとなる線を引くことができます
よって点A→辺→点Bの最短となる経路は
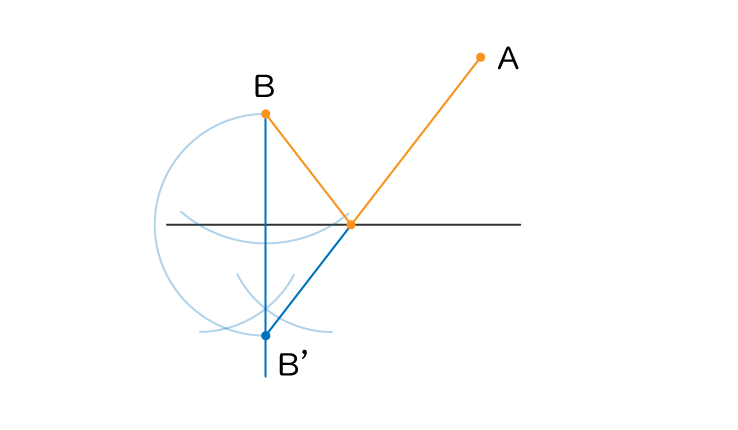
こうなります

コーチ
最短の問題をはじめて見たときは解き方にちょっと感動するよね
等しい距離
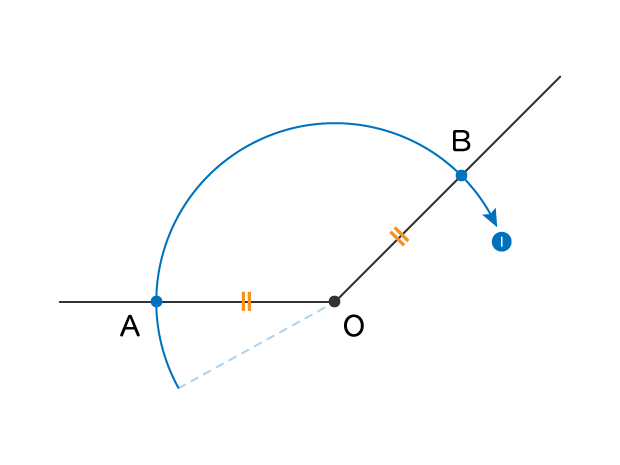
最後は当たり前といえば当たり前のテクニックです
同じ円の半径であれば常に等しい
このテクニックを使うときもちょくちょくあるので覚えておきましょう!
問題文では
といった書き方をされます
作図の解き方のコツ
(さて、軽い気持ちでこの記事を書き始めてすでに少し後悔しています)
だいぶ長くなってしまいましたが、テクニックの紹介が終わりましたので
次は、作図を解くときのコツを2つ紹介します
- 問題文を分解
- 完成図をフリーハンドで書き込む
問題文を分解しよう
問題文の例
右の図のように、線分AB,BCがあります。線分ABと線分BCのどちらにも接する円のうち、線分ABとは点Pで接する円を、コンパスと三角定規を使って作図しなさい。ただし、作図するために書いた線は、消さないでおきなさい。
これを分解しましょう
問題文の例を分解
右の図のように、線分AB,BCがあります。
・線分ABと線分BCのどちらにも接する円
のうち、
・線分ABとは点Pで接する円
を、コンパスと三角定規を使って作図しなさい。ただし、作図するために書いた線は、消さないでおきなさい。
この問題文には作図する条件が2つ書いてあります
- 線分ABと線分BCのどちらにも接する円
- 線分ABとは点Pで接する円
問題文からこの情報だけを下線を引いたり、丸で囲ったりして
問題文を分解しておくと難解に思える作図の問題文もシンプルに見えてきます
完成図をフリーハンドで書き込もう
作図の手がかりがつかめないときはこの方法がおすすめ
作図の答えは解答用紙に書きますが、問題文にも作図の図形が書いてあります
なるべく正確に丁寧に完成図を書き込みましょう
これは作図だけではありませんが
数学で解き方の手がかり見つからないときは
分かっている情報を書き込んで手を動かす方がきっかけを見つけやすいです
まとめ
作図のテクニック4つを紹介しました
- 線の二等分線(中点)
- 角の二等分線
- 垂線
- 等しい距離
また、解き方のコツも2つ書きました
- 問題文を分解する
- 完成図を書き込む
以上が北辰テストで作図を解くために必要なことです
少しでも作図の苦手意識がなくなることを願っています(誰に?w)


