このページのもくじ
平均点とボーダー
| 偏差値 | 得点 |
|---|---|
| 50 (平均点) | 46.9点 |
| 60 | 65点 |
| 65 | 74点 |
| 70 | 82点 |
問題と正答率
| 大問1 | 単元 | 正答率 |
|---|---|---|
| (1) | 文字式の加減 | 96% |
| (2) | 正負の四則演算 | 92% |
| (3) | 文字式の四則演算 | 88% |
| (4) | 文字式の乗除 | 87% |
| (5) | 連立方程式 | 87% |
| (6) | 素因数分解 | 70% |
| (7) | 反比例(値) | 70% |
| (8) | 空間図形(平行) | 47% |
| (9) | 平行線と角 | 87% |
| (10) | 箱ひげ図 | 34% |
| (11)① | 一次方程式(文章題) | 49% |
| (11)② | 一次方程式(文章題) | 33% |
| 大問2 | 単元 | 正答率 |
|---|---|---|
| (1) | 作図 | 38% – 26% |
| (2) | 確率 | 56% |
| (3) | 正負の数(選択) | 65% |
| (4) | 空間図形(体積) | 5% |
| (5)① | 文字式(規則性) | 94% |
| (5)② | 文字式(規則性) | 27% |
| 大問3 | 単元 | 正答率 |
|---|---|---|
| (1) | 一次関数(基礎) | 36% |
| (2) | 一次関数(応用) | 25% |
| 大問4 | 単元 | 正答率 |
|---|---|---|
| (1) | 証明 | 14% – 56% |
| (2) | 平面図形(角度) | 16% – 14% |
| (3) | 平面図形(面積) | 0% |
手書きで解説するから字の汚さは大目に見てください

賢い犬
大問1
(1)
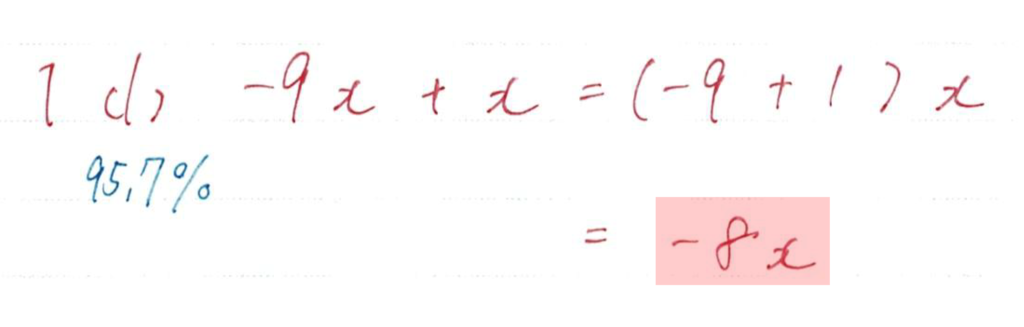
基礎の基礎問題ですが、正答率は100%ではありません。
「見直し」や「二度解き」などして確実に4点を取りましょう。
(2)
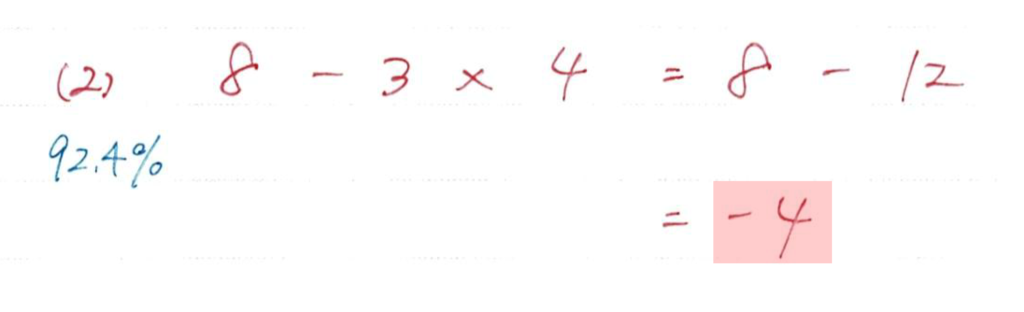
四則演算(足し算・引き算・かけ算・わり算)を含んだ正負の計算
(3)
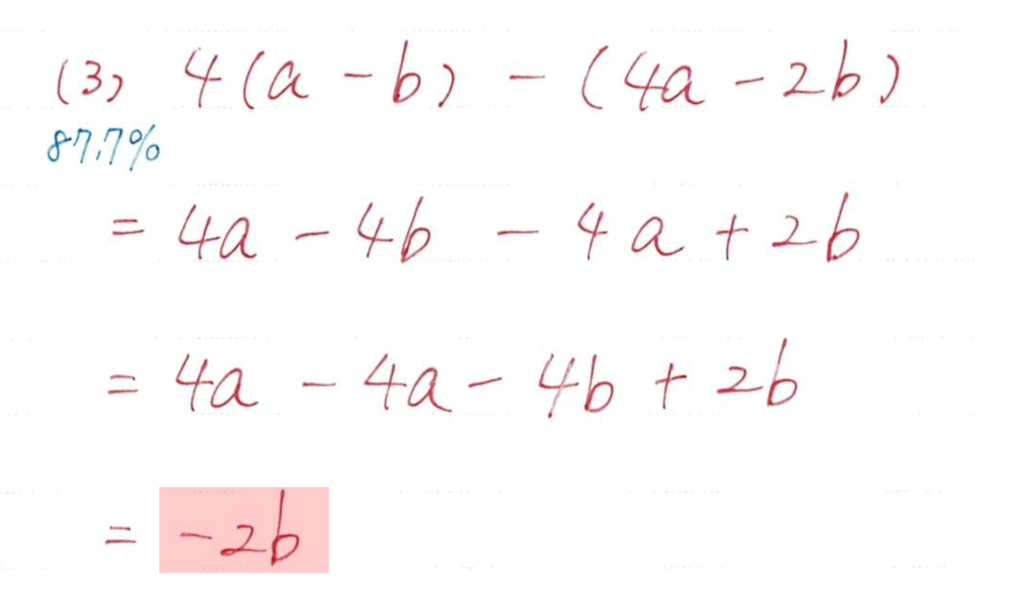
分配法則を丁寧にしましょう
特にカッコの前にマイナスがついているときは
カッコ内の符号が変わるので要注意
(4)
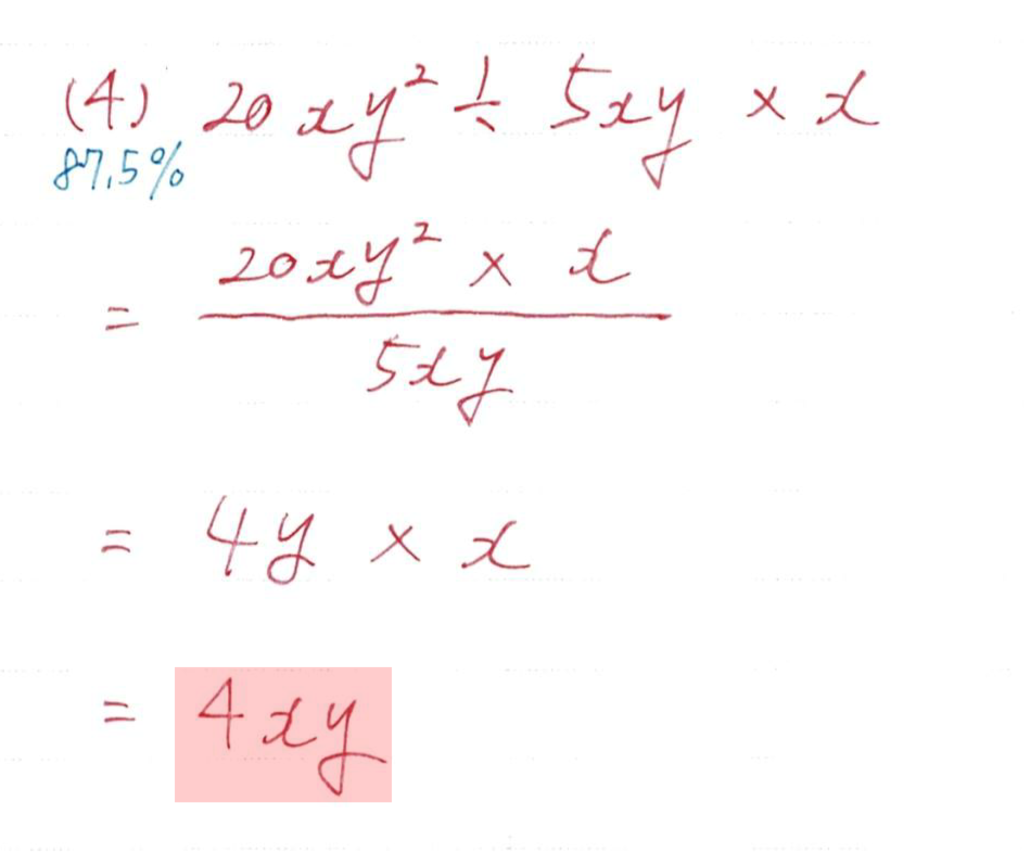
計算ミスが多い問題
こちらは「違う方法で二度解き」が有効です
- 分数に直して計算する方法
- 解きやすい順番で計算する方法
10%以上の生徒が間違えていることを頭にいれて必ず見直しをしましょう
(5)
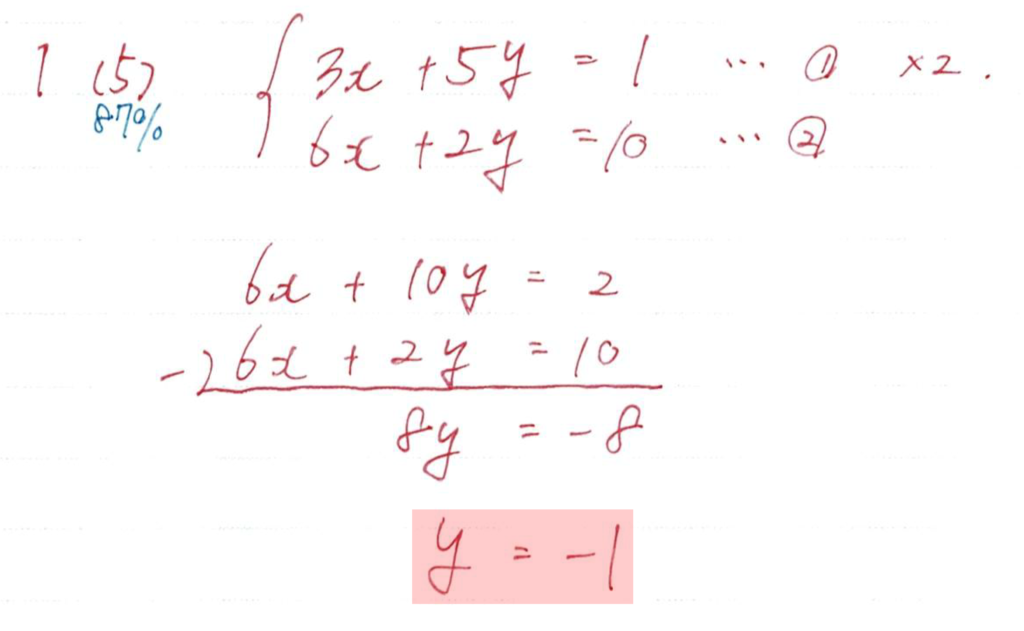
みんな大好き連立方程式ですね
北辰テストではだいたいが加減法で解きやすい形の出題が多い
まずは係数を合わせて1つの文字を削除しましょう
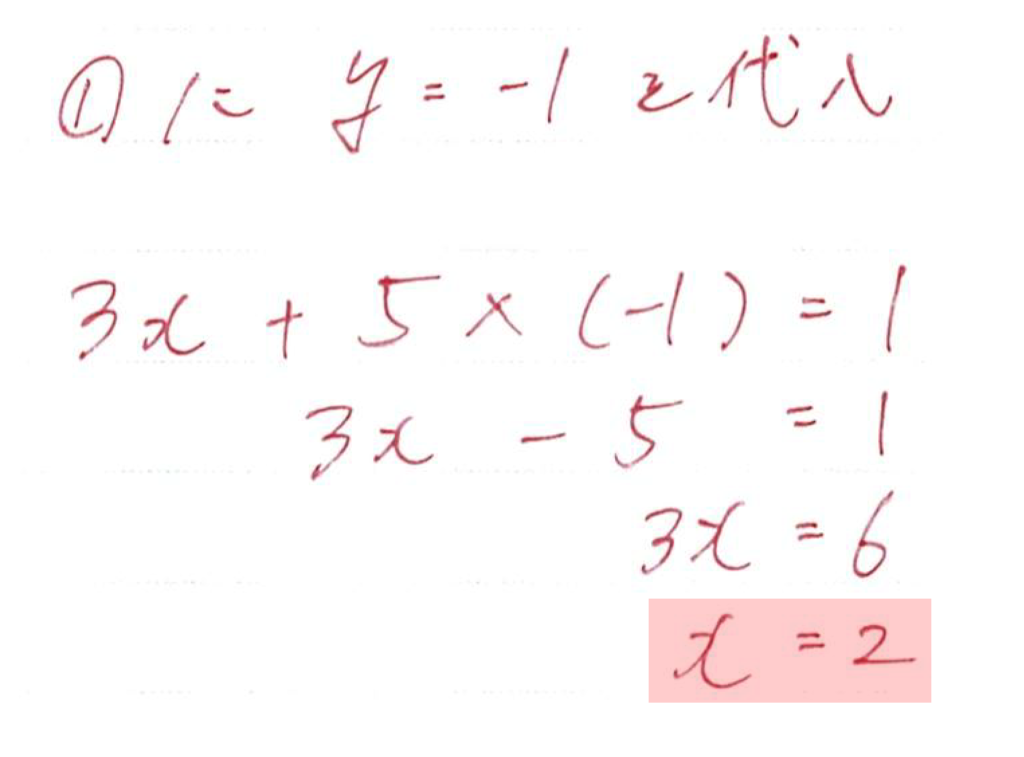
答えが出たら必ず検算をしていきましょう!
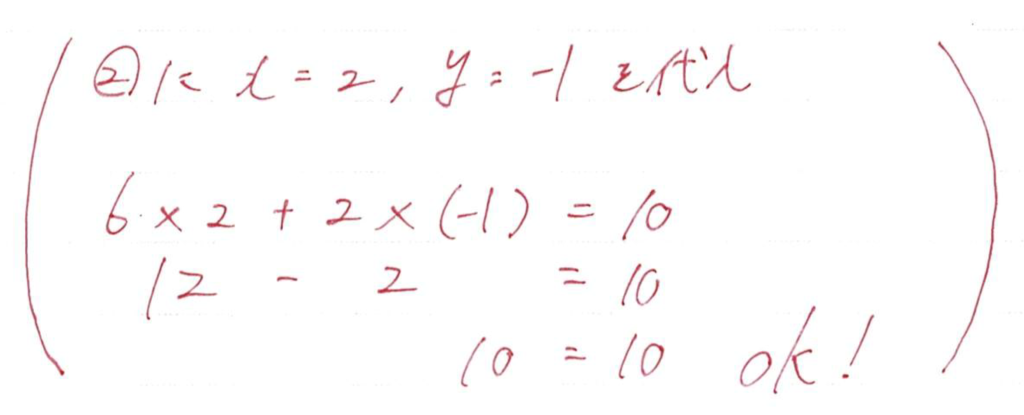
これができるから連立方程式は100%正解を確認できますね
おっと、この問題でも13%の生徒が間違えている、、、
(6)
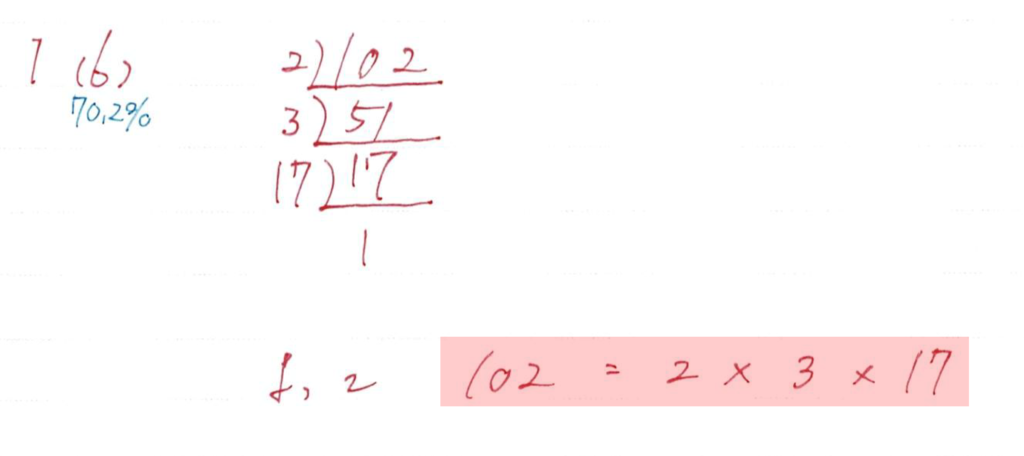
素因数分解はたまーに出てきます
素数とは
1とその数以外の約数を持たない数のことです。
例)2,3,5,7,11,13,17,19,23.29…..
素因数分解したあとは答えの書き方に注意しましょう
- 数字の小さい順にかけ算の形で書く
- 同じ数字が出てきたら累乗の形でまとめる
(7)
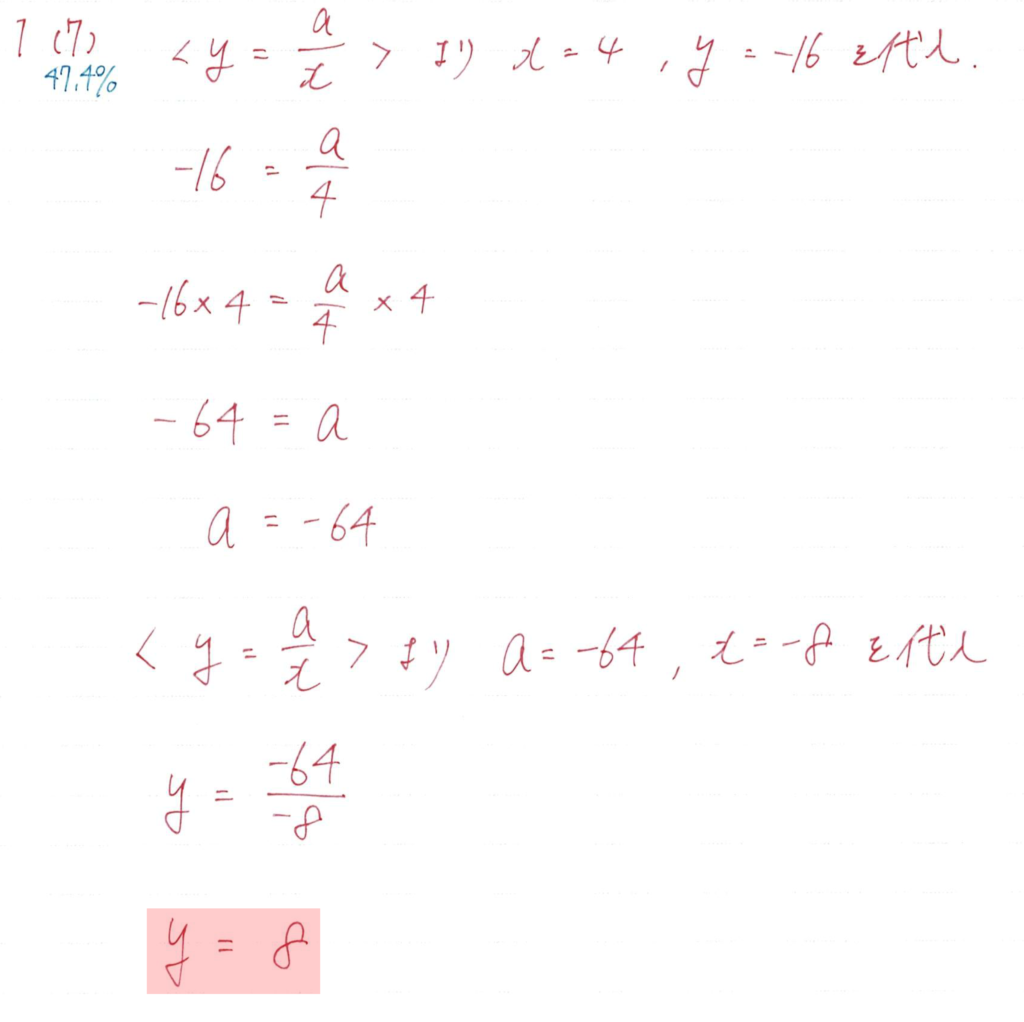
反比例は公式覚えとけば楽勝です
苦手な生徒が多いため、正答率は大問1の中でもかなり低め
しっかり解くコツとしては
- 必ず公式を書く
- 代入する値を丁寧に確認する
比例・反比例・一次関数・二次関数といった関数の問題は
覚える公式が多少違うだけで、解き方の本質は同じパターンです
なぜ間違いが多い?
しっかり公式や途中式を書かない生徒が一定数いるからです。公式を書かずに頭の中で代入して計算する人がいます。「公式を思い出し」「代入して」「計算する」を同時にやるとミスの確率がぐっとあがります。かわいそうですね。
(8)
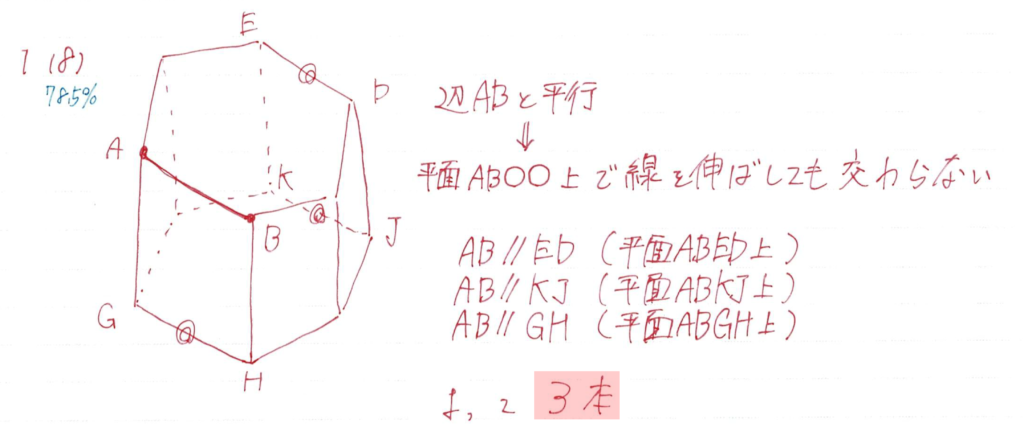
図下手すぎwwwwwwwwwwwwwwwwww
平行な線を探す問題ですね
この問題で大切な考え方は「平面」で考えること
平行な線は
- 同一平面上にあり
- 延長しても決して交わらない
イメージとしては同じクラスだけど絶対こいつとは仲良くなれない生徒みたいな感じです
いや、わかりにくい例えだな

賢い犬
(9)
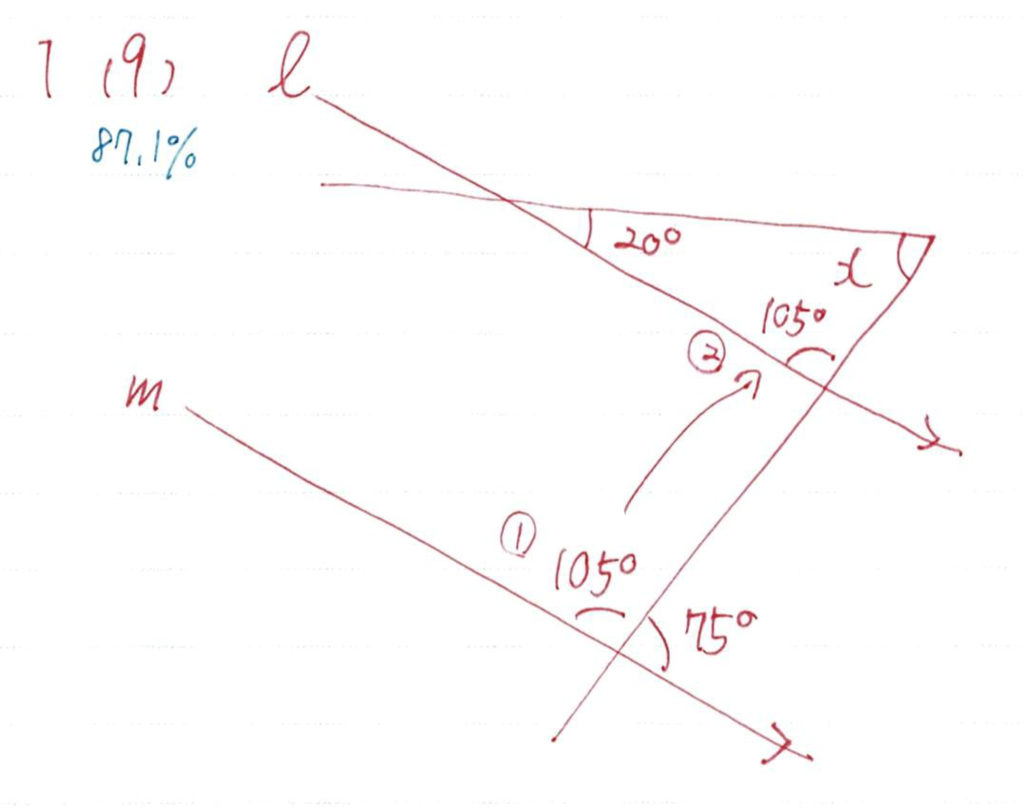
平行線と角の問題ですね今回は
- 一直線上
- 同位角
- 三角形の内角の和
こちらを使ってひとつひとつ書き込みながら丁寧に計算していきましょう

(10)
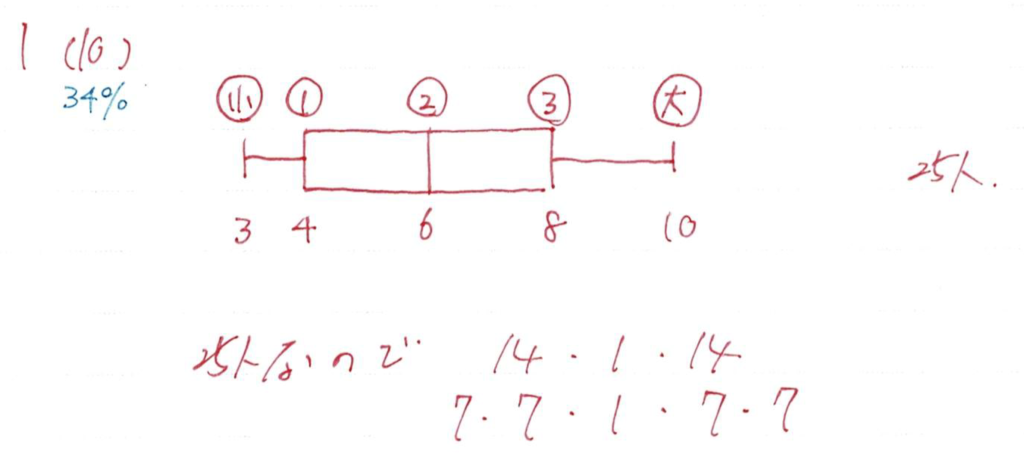
箱ひげ図は
- データを小さい順に並べて
- 数を基準に4つに分けた
データのばらつきを見る単純な問題です
全体は25人なので、箱ひげ図のどこに何人いるのか確認していきます

選択肢の「ア」「ウ」は正誤の判断はわかりやすいですね
選択肢の「イ」については
極端な反例を考えてみましょう
第2四分位範囲~最大値までの範囲で確定している値は最大値の10点です
第3四分位数は8点なので、例えば他の13人がすべて8点でもこの箱ひげ図は成り立ちます
よって「イ」は誤りであることがわかります
こちらも参考に
(11)
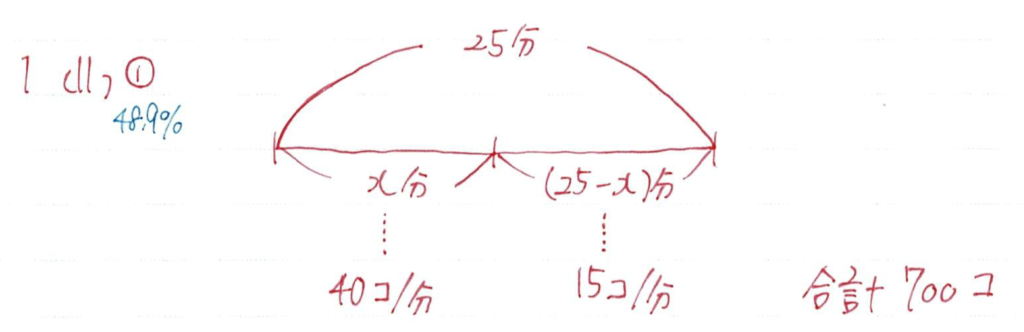
方程式の文章問題ですね
問題文からわかる情報から図と表を作成していきましょう
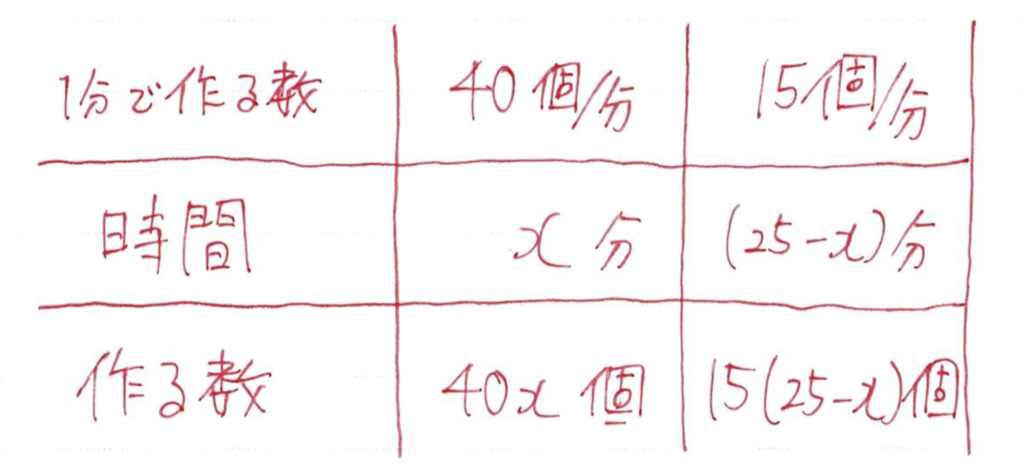
こういった問題では「単位」が大切になります
たとえば
1分あたり◯個つくる場合の単位は「個/分」になります
この単位をヒントに式を組み立てるとミスが減ります
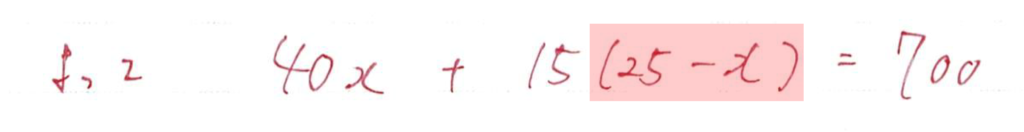
次に②の答えを考えます
北辰テストではここでよくひっかけをします
問題文をしっかり読んでいますか?という北辰テストからの問いかけですね~
正答率が①は49%なのに②が33%ということは、問題文を正しく読めていない生徒がとても多い

②を解く前に必ず「求める値」を確認しましょう
このとき、表を書いている生徒はどの部分を求めれば良いのか簡単に確認できるため正答率はあがります
表を書かない、図を書かない生徒は残念ですね
大問2
(1)

今回の作図は基礎問題でしたね
(2)
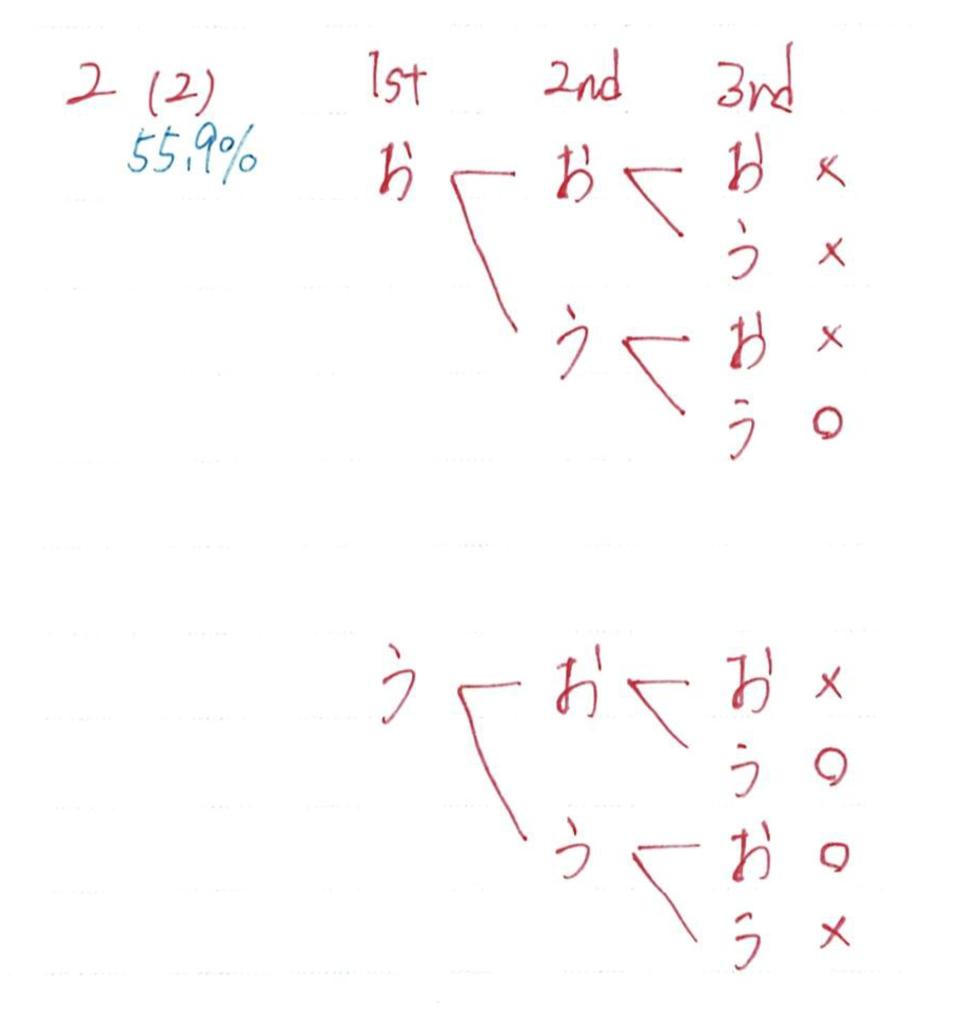
北辰テストの確率問題の難易度はかなり簡単です
今回は「コインの裏表」についての問題でしたね
表と裏を漢字で書くと大変なので、表は「お」、裏は「う」と書くと樹形図は書きやすいと思います
樹形図からわかる情報を公式に代入していきましょう
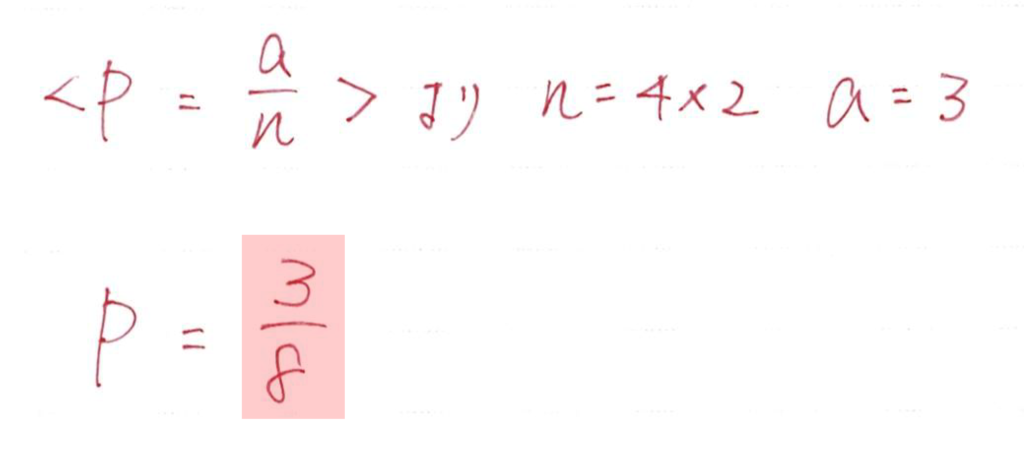
(3)

正負の数の選択問題ですね
ひとつひとつ条件からわかることを書き出して
確定できる正負を考えていきましょう
②と③でbが2倍になると負になることから
bは負であることが確定します
また、①からbが負の場合
a正、b負、c正
または
a負、b負、c負
のどちらかに絞られます
②からすべて足し算したときに正となっていることから
a正、b負、c正
が正解とわかります
(4)
大問2の(4)の図形問題は正答率が低い傾向があります
今回も10%以下であるため、偏差値70以上を目指す生徒以外は解かなくても大丈夫です
まず、問題文からわかる条件を図にして数値を書き込みます
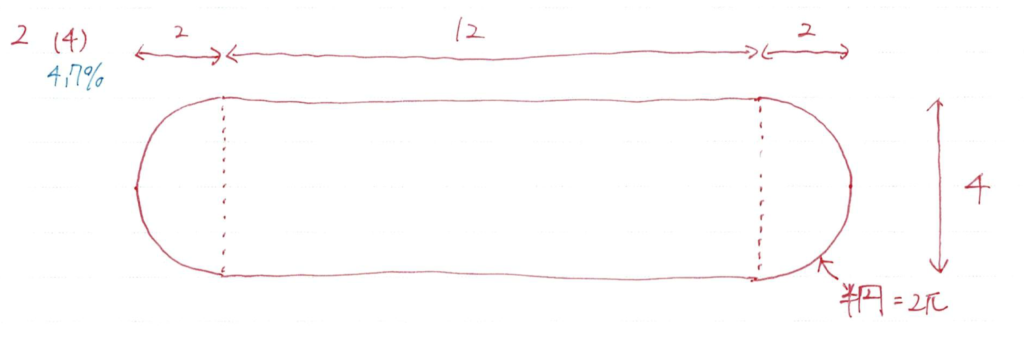
長方形の両端に半円をくっつけたものを2枚組み合わせて立体図形を作成します
図形を書くのが難しいので平面図と立面図で考えていきましょう
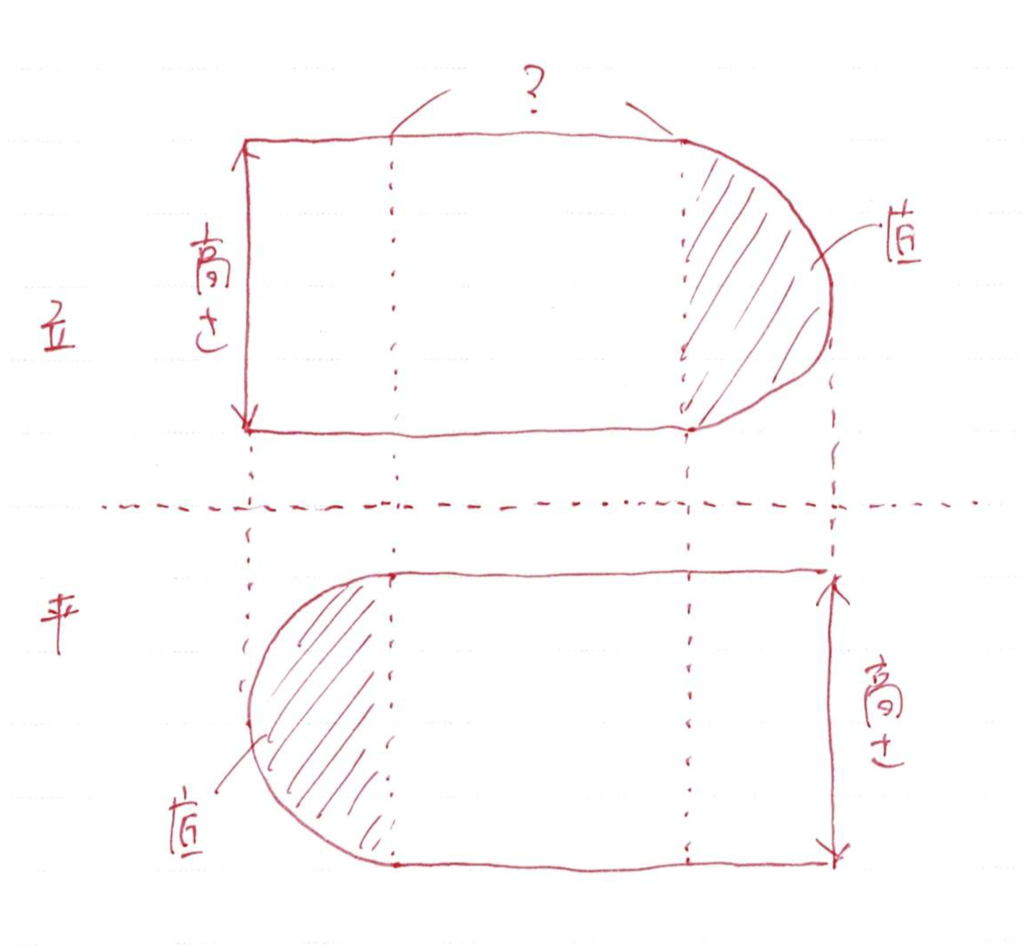
上の図から
両端の体積は底面を考えれば簡単に求めることができそうですね
ただ、中央の底面部分の幅がわからないので、こちらを考えていきましょう
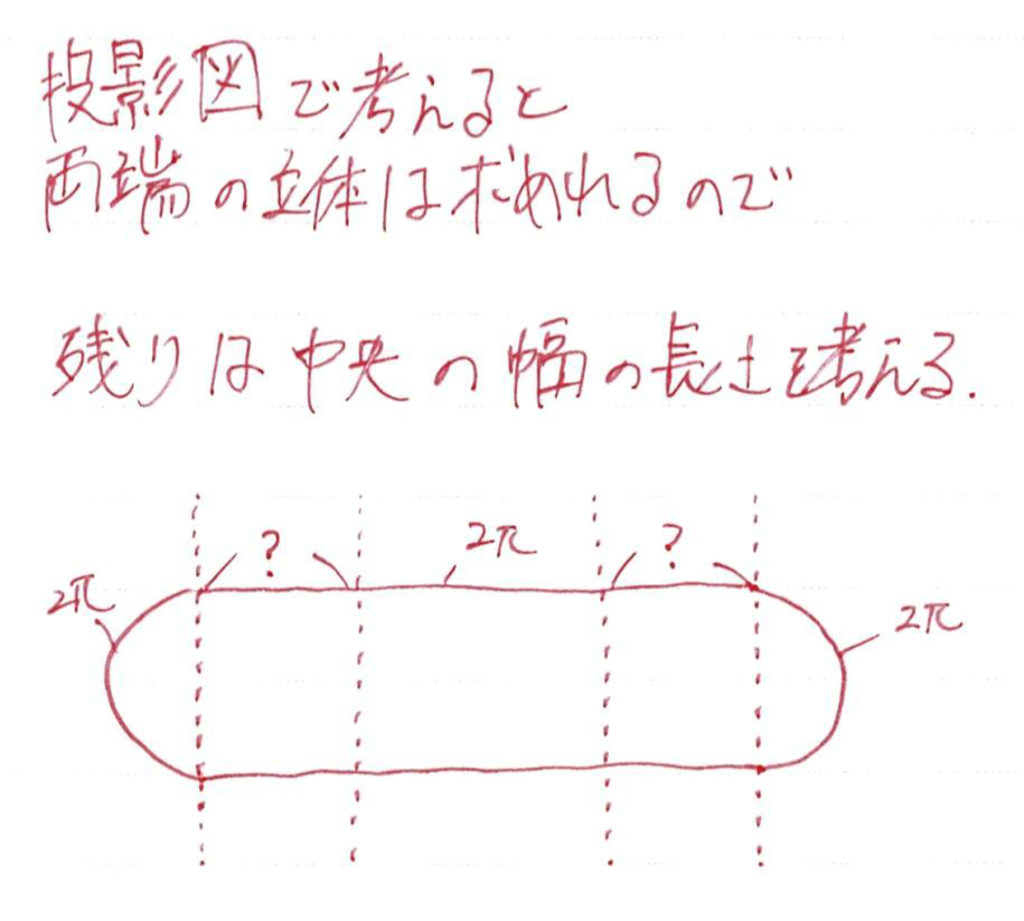
少し複雑なので、わかっている長さとわからないところを図にしておくといいでしょう
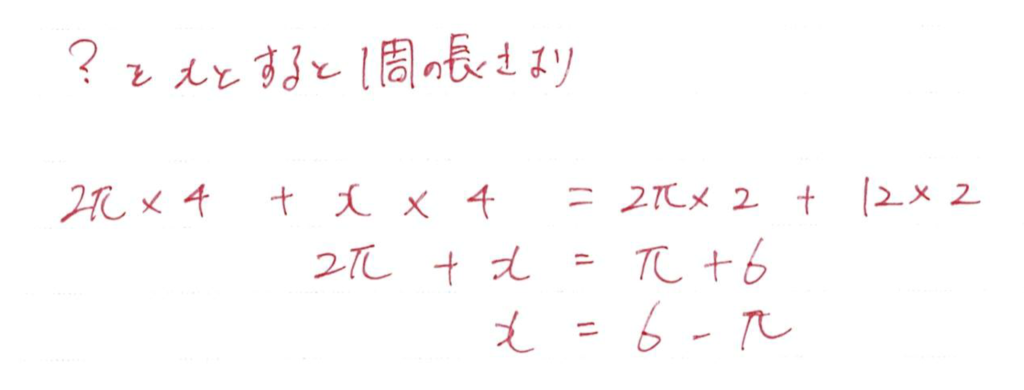
1周の長さはわかっているので、方程式を立てていきます

両端なので最後に2倍しています
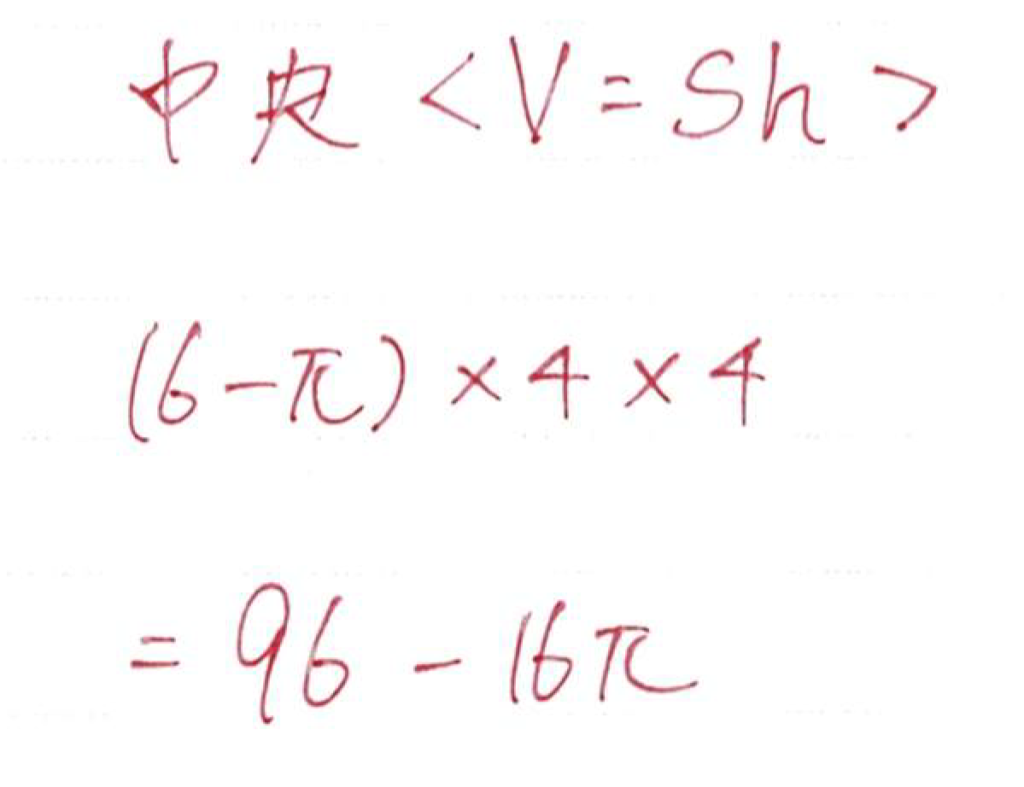
中央の幅と奥行きから底面の面積がわかり、あとは高さをかけ算しました

面白い答えになりましたね
πが消えて整数が答えでした
別解として、片方の半円柱部分を90度回転させて考える方法もあります
どちらにしても中央部分の幅を考える必要があるので
こういった問題では
「どこを求めれば答えにたどり着けるのか」をしっかり考える練習をしていきましょう
(5)①
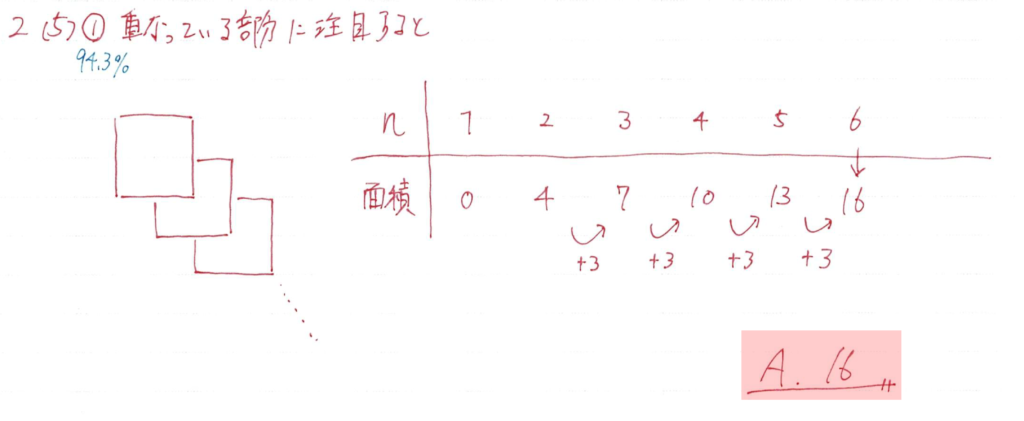
問題文の表から増加する割合が等しいことを読み取れる
(5)②
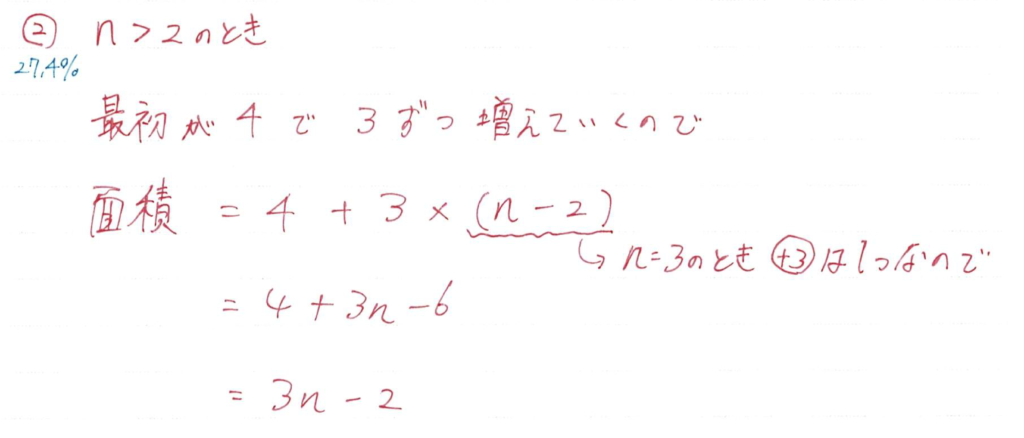
表から「最初」と「それ以降」を考えていきます
+3がどんどん追加されていきます
nが3のとき(+3)はひとつなので
(+3)が(nー2)個ずつ増えていくことを見抜けるかどうかがポイントです
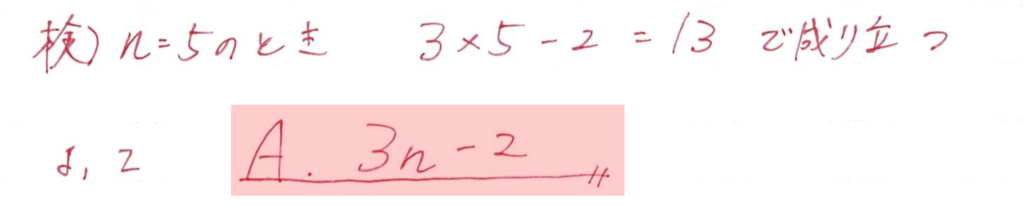
表を参考にnに値を入れて成り立つかどうかをしっかりと検算していきましょう
大問3
(1)
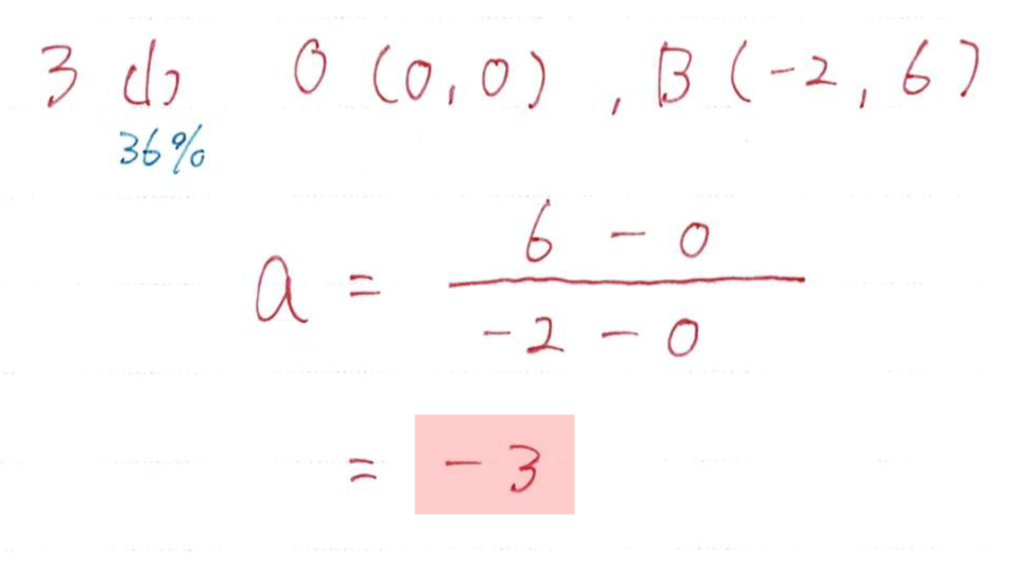
傾きを求める問題ですね
公式に当てはめて求めるのがベターでしょう
また、傾きはxが1増えたときにyの増加量なので
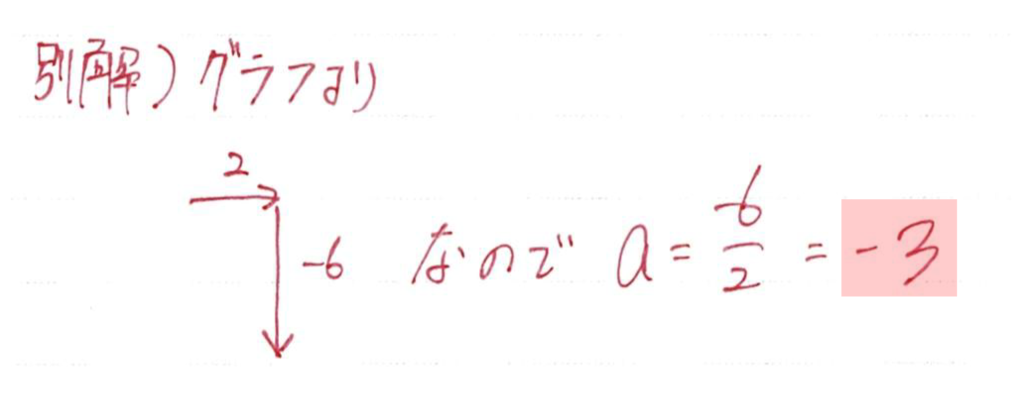
グラフから読み取っても簡単に求めることができます
xが2増えたら、yの増加量はー6なので
xが1増えたら、yの増加量は-3とわかりますね
応用問題を解くときには意外とこちらの考え方が役に立つことが多いです
(2)
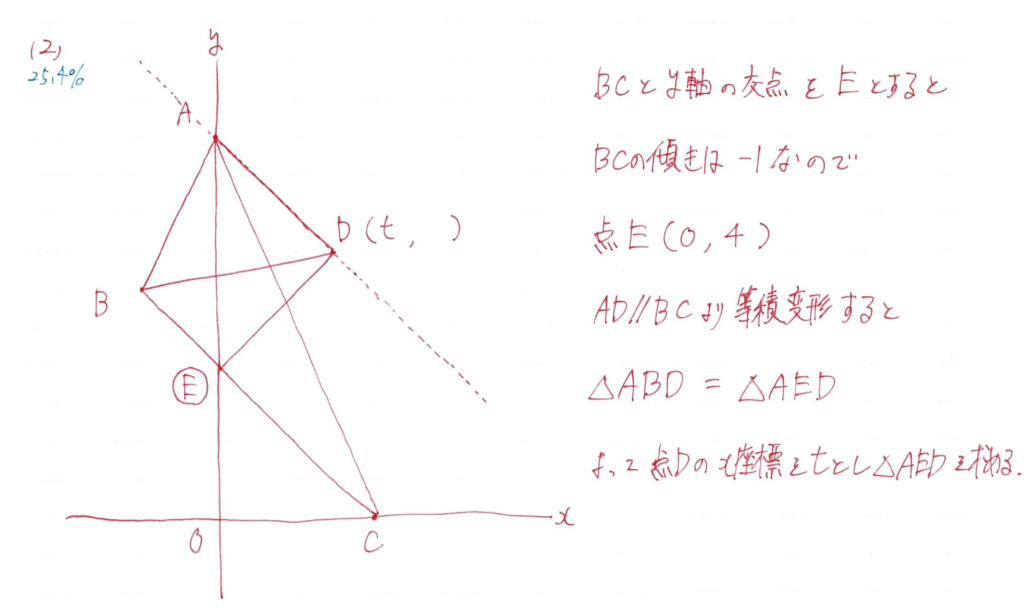
関数と図形の問題ですね
面積や平行などの言葉が問題文で出てきたら「等積変形」を使うのでは?
と考えておきましょう
問題文から面積がわかる△ABDは底辺も高さも簡単にはわかりません
そこで平行線を利用して△ABDを等積変形(点B→点Eに移動)させます
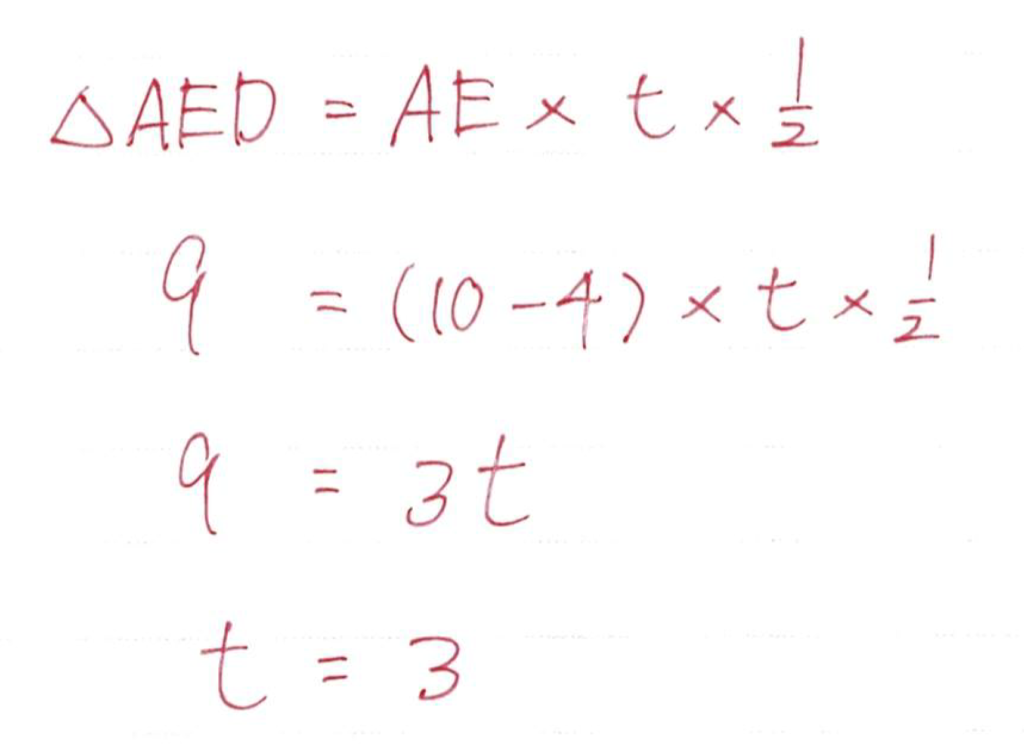
あとは不明な部分をtと置いて面積の方程式をつくります

点Aがy座標10なので、そこからx軸方向に+3動けばy座標は-3されるので点Dのy座標は7とわかります
いつもはもう少し難しい問題が出題されますが、今回は比較的取りやすい問題でしたね
大問4
(1)
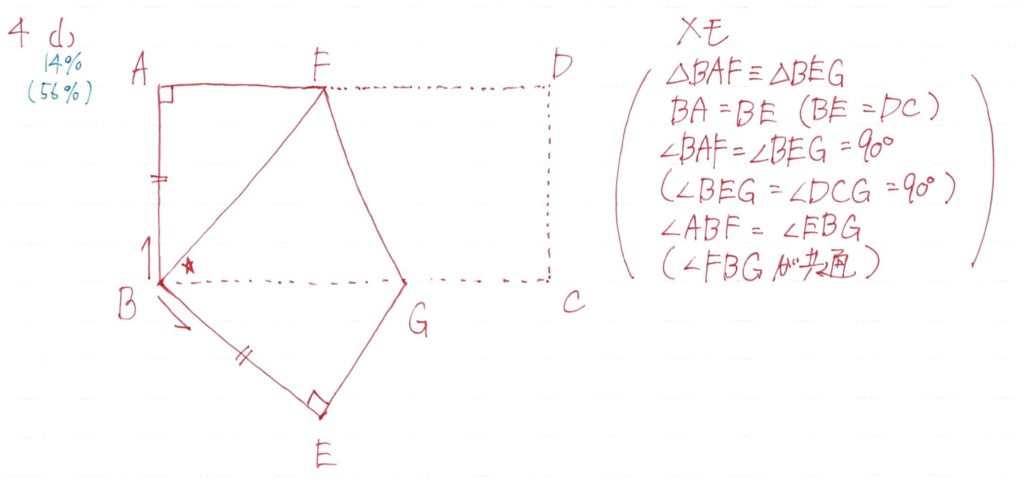
折返しの図形の証明ですね
証明のコツは答えまでの道筋をメモしたあとに書き始めることです
そうすることでアルファベットの順番ミスなどを減らすことができます

折返しの証明では
折り返して重なる辺と角度が等しくなることを仮定で宣言しておく必要があります
(2)
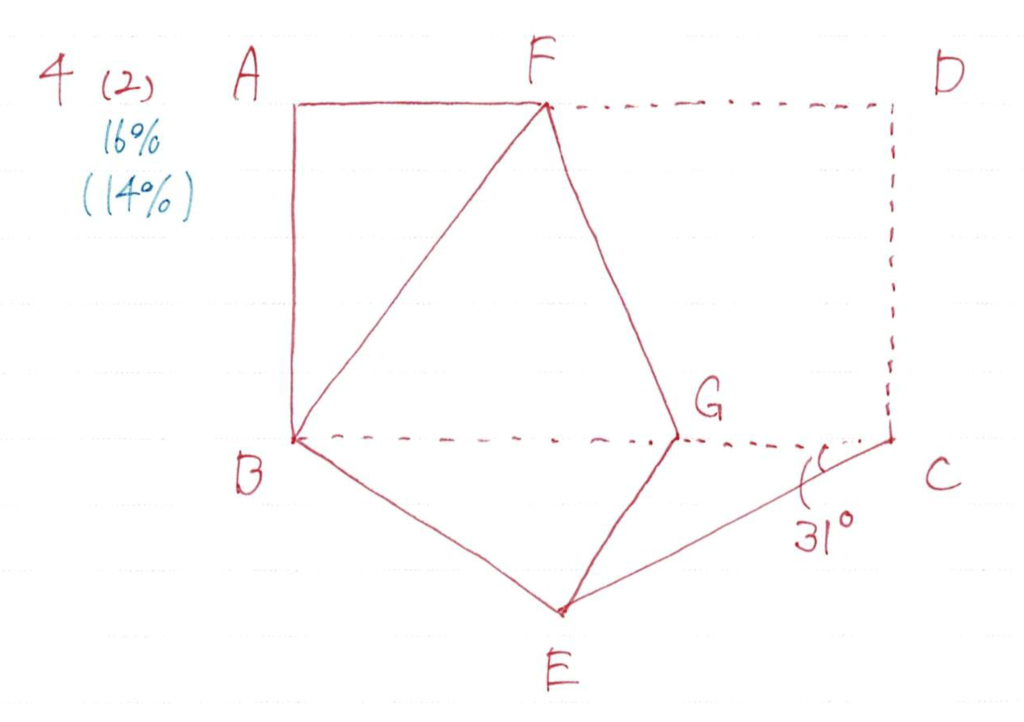
角度を求める問題ですね
今回は解き方の過程まで記述する必要があります
記述のコツは採点している人に「今はここを説明していますよ」とわかるように記述することです
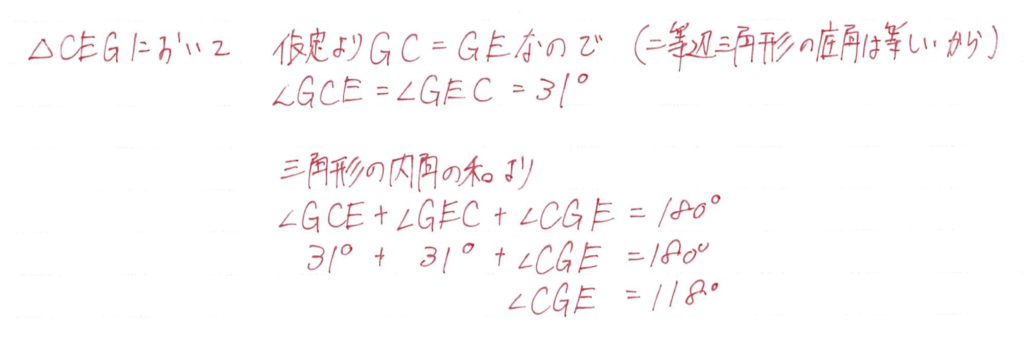
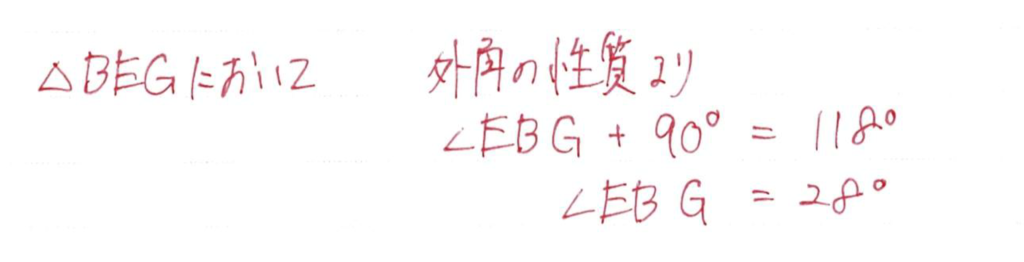

「△ABCにおいて~」のように今はこの三角形について説明していますと書くといいでしょう
理由を書くときは「〇〇より~」と書きましょう
(3)
さて、ラスボスです
今回のラスボスは過去最高の正答率0%です
しかし、この問題は大量に等積変形を使用するので、偏差値70以上を目指している生徒は
力をつける上でもしっかりと解き直しておきましょう
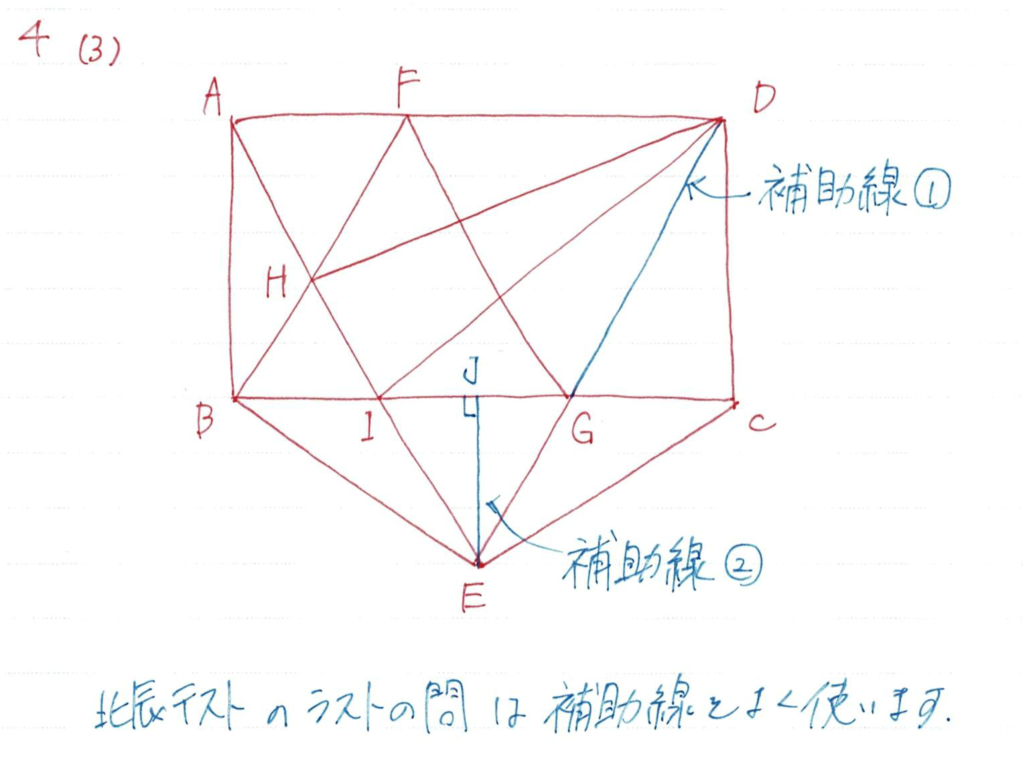
わたしが記憶している限りでは最後の問題は補助線を使います
補助線を入れるポイントは
- 等積変形用
- 合同な図形用
このパターンがほとんどになります


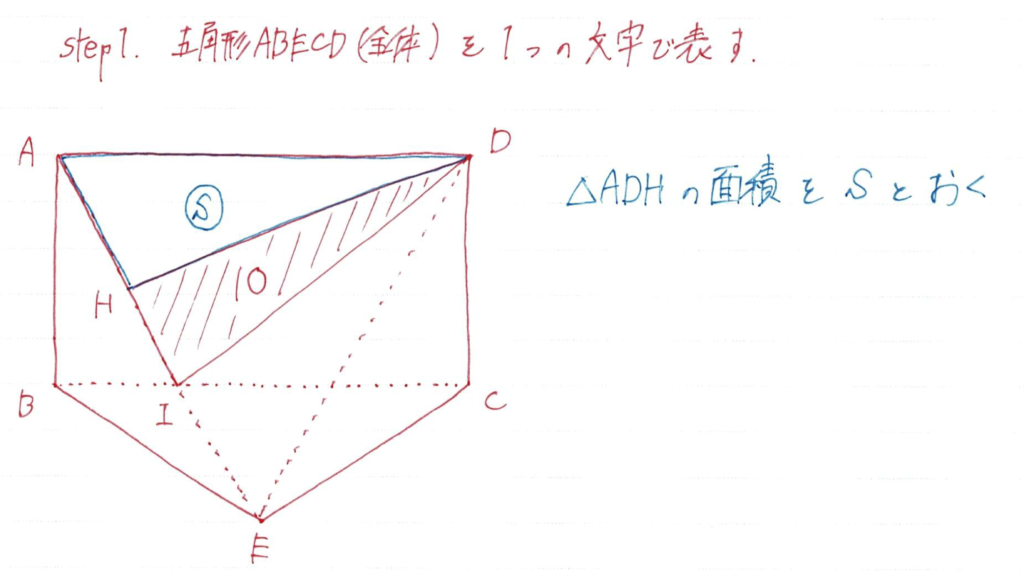
面積の問題ではなるべく小さい部分を「S」として考えるのがベターです
今回は長方形の半分をSで表すことができるので△ADHをSとしています

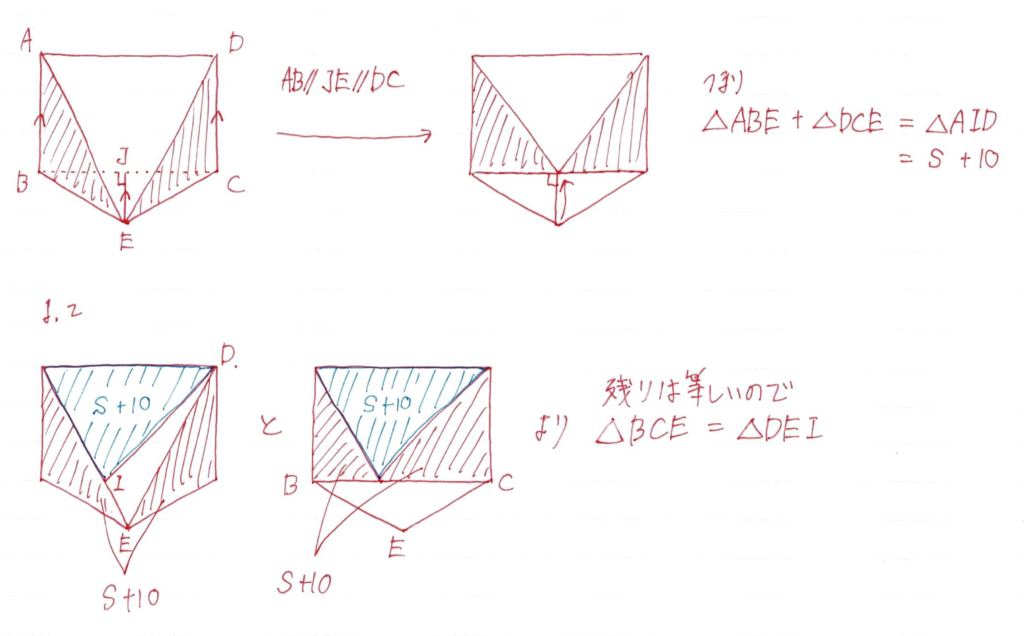
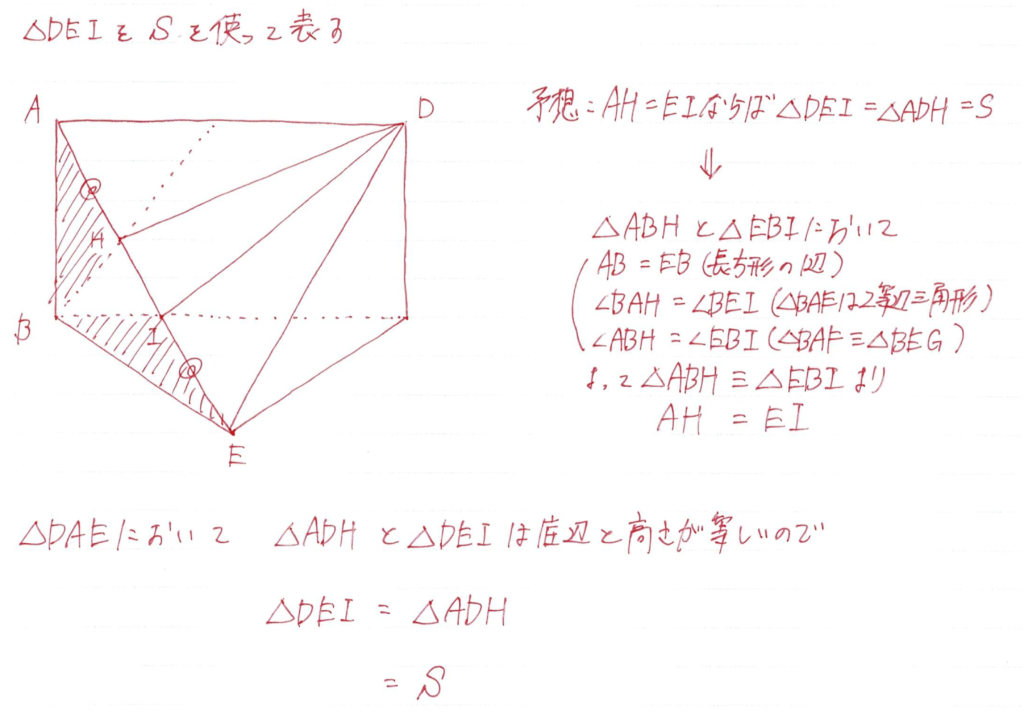
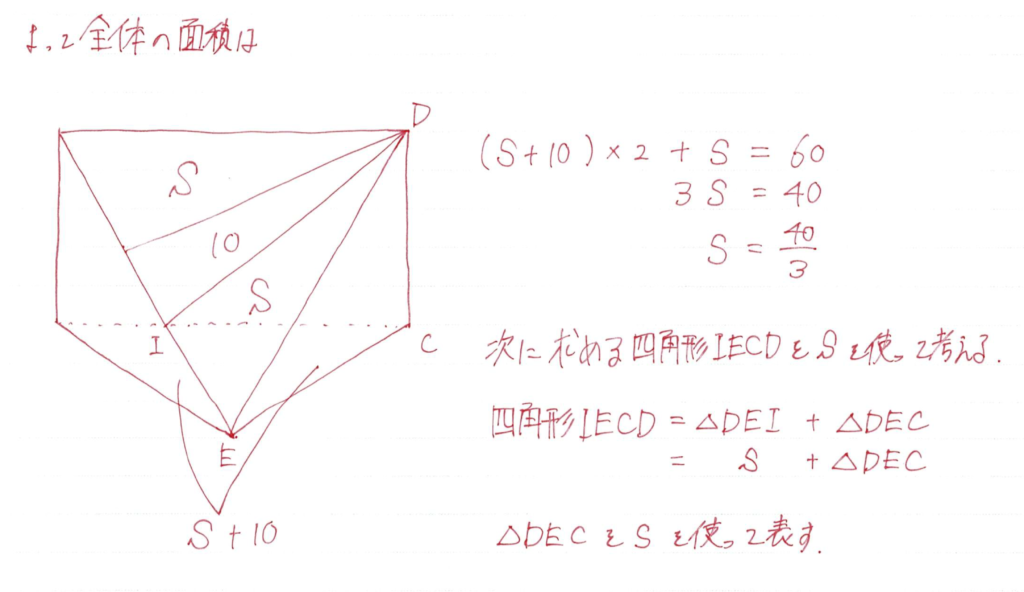
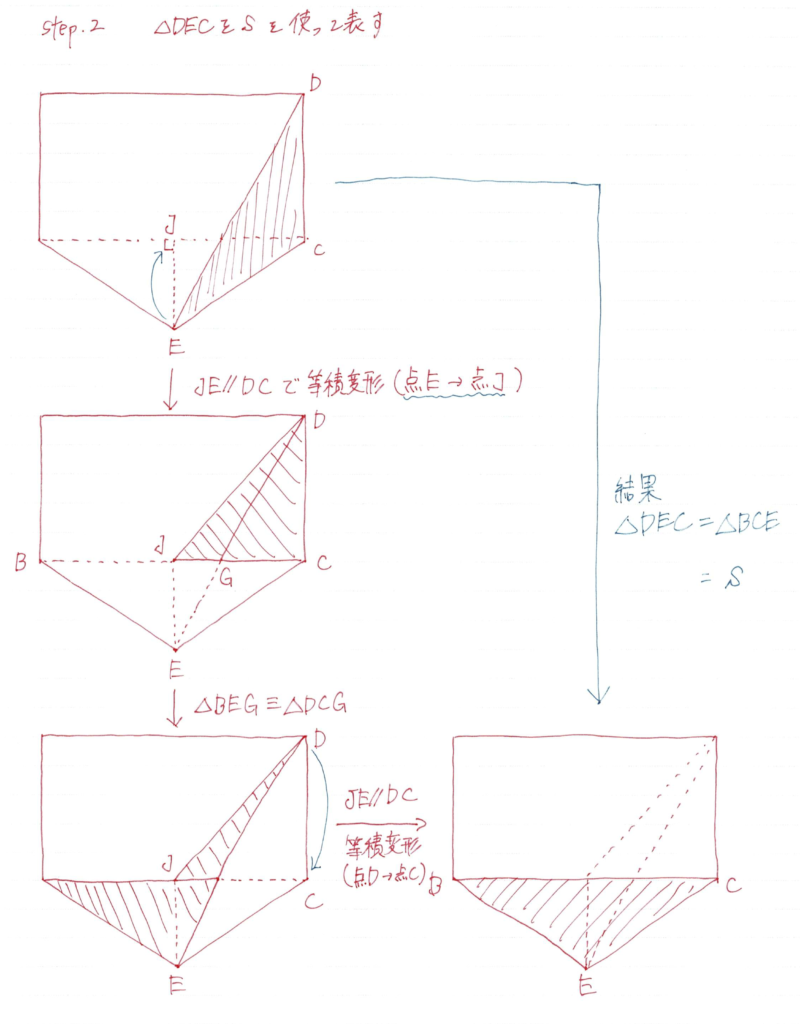
ここの等積変形は合同も利用していますね
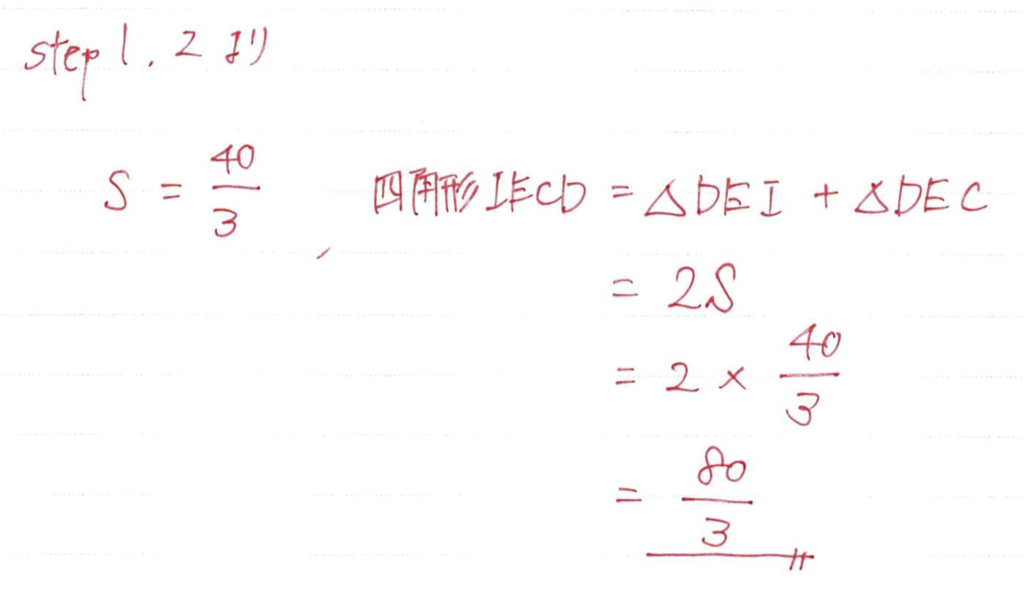
計算自体はあっという間におわります
それにしても面白い問題ですね!!
選択問題に挑戦する生徒へ
数学の選択問題は通常の難易度から跳ね上がります
中学3年分の数学の基礎を固めたら
できるだけ早く難しい問題に触れておきましょう








